


Next: Markov Chain Monte Carlo
Up: MCMC and EM Algorithms
Previous: MCMC and EM Algorithms
The goal of Bayesian inference is to find the model parameters
denoted by 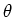 , based on the observed data denoted by
, based on the observed data denoted by 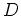 .
Assume the a priori distribution of the parameters is
.
Assume the a priori distribution of the parameters is
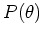 and the distribution of the data is
and the distribution of the data is 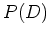 , then
the joint probability of both the data and parameters is
, then
the joint probability of both the data and parameters is
The posterior distribution of the model parameters can be
obtained according to Bayesian theorem:
where
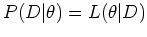 is the likelihood function
of the parameters
is the likelihood function
of the parameters 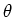 , given the observed data
, given the observed data 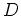 . This
equation can be interpreted as
. This
equation can be interpreted as
In a maximum-likelihood problem, the goal is to find 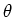 that
maximizes the likelihood
that
maximizes the likelihood 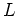 :
:
which can be obtained by solving the likelihood equation:
Bayesian inference can be used to find any feature of the
posterior distribution 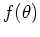 , whose posterior expectation is
, whose posterior expectation is
The integration in this expression is likely to be of high dimensions,
and in most applications, analytical evaluation of
![$E[f(\theta)\vert D]$](img14.png) is
impossible. In such cases, Monte Carlo integration can be used, including
Markov Chain Monte Carlo (MCMC).
is
impossible. In such cases, Monte Carlo integration can be used, including
Markov Chain Monte Carlo (MCMC).



Next: Markov Chain Monte Carlo
Up: MCMC and EM Algorithms
Previous: MCMC and EM Algorithms
Ruye Wang
2006-10-11
![]() , based on the observed data denoted by
, based on the observed data denoted by ![]() .
Assume the a priori distribution of the parameters is
.
Assume the a priori distribution of the parameters is
![]() and the distribution of the data is
and the distribution of the data is ![]() , then
the joint probability of both the data and parameters is
, then
the joint probability of both the data and parameters is
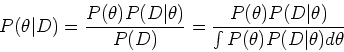
![]() , whose posterior expectation is
, whose posterior expectation is
![\begin{displaymath}E[f(\theta)\vert D]=\int f(\theta) P(\theta\vert D) d\theta
=...
...(D\vert\theta)d\theta}{\int P(\theta) P(D\vert\theta) d\theta} \end{displaymath}](img13.png)