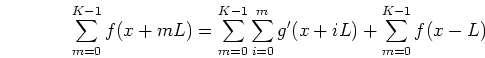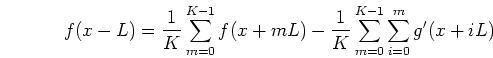Next: Numerical Derivative
Up: motion
Previous: Restoration by Inverse Filtering
To simplify the problem we assume:
- The image is blurred by linear motion:
where 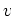 is the constant speed of the motion and
is the constant speed of the motion and 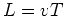 is the distance traveled during the exposure time
is the distance traveled during the exposure time 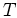 .
.
- The width of the image
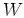 is a multiple of
is a multiple of 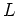 :
:
We next introduce a new variable 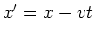 , and have
, and have 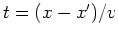 and
and
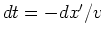 . Moreover, the integral limits
. Moreover, the integral limits 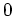 and
and 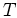 for
for 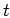 become,
respectively,
become,
respectively, 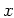 and
and 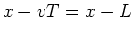 for
for 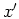 . Now the image becomes
. Now the image becomes
where
For convenience, we will ignore the constant factor 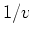 .
.
As the motion distortion is essentially an integration
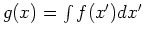 ,
to restore
,
to restore 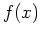 from
from 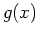 , we can simply differentiate
, we can simply differentiate 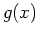 :
:
and restore the original signal 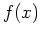 as
as
Note that above equation only recovers 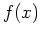 inside the interval
inside the interval
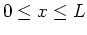 .
.
To recover the rest of 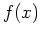 , we replace
, we replace 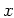 by
by 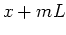 for
for
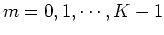 and apply the above relationship recursively
and apply the above relationship recursively
Here 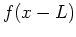 represents the segment of signal of length
represents the segment of signal of length 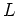 that moves
from outside the image into the image during the exposure time
that moves
from outside the image into the image during the exposure time 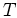 . If
. If
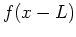 is known, for example, if we can assume
is known, for example, if we can assume
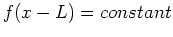 (e.g.,
uniform background), then the original signal
(e.g.,
uniform background), then the original signal 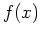 over the entire interval
over the entire interval
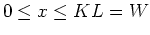 can be obtained by evaluating the above equation at
can be obtained by evaluating the above equation at
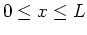 for all
for all
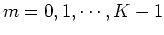 .
.
However, if we cannot assume
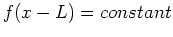 , it need be estimated. As
the above equation is valid for
, it need be estimated. As
the above equation is valid for
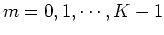 , we actually have
, we actually have 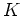 equations which can be added up to give
equations which can be added up to give
which can be solved for 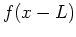
The first term on the right is an average of 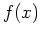 over the entire range of
the image and can be estimated by the average of
over the entire range of
the image and can be estimated by the average of 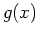 .
.



Next: Numerical Derivative
Up: motion
Previous: Restoration by Inverse Filtering
Ruye Wang
2003-10-02
![]() , and have
, and have ![]() and
and
![]() . Moreover, the integral limits
. Moreover, the integral limits ![]() and
and ![]() for
for ![]() become,
respectively,
become,
respectively, ![]() and
and ![]() for
for ![]() . Now the image becomes
. Now the image becomes
![]() ,
to restore
,
to restore ![]() from
from ![]() , we can simply differentiate
, we can simply differentiate ![]() :
:
![]() , we replace
, we replace ![]() by
by ![]() for
for
![]() and apply the above relationship recursively
and apply the above relationship recursively
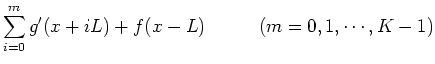
![]() , it need be estimated. As
the above equation is valid for
, it need be estimated. As
the above equation is valid for
![]() , we actually have
, we actually have ![]() equations which can be added up to give
equations which can be added up to give