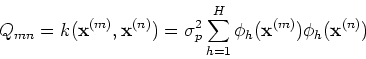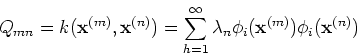Next: Appendix A: Conditional and
Up: Gaussiaon Process
Previous: Nonlinar Regression
The function
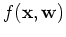 can be written as
can be written as
If the prior distribution of the weights 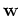 is zero-mean Gaussian:
is zero-mean Gaussian:
then the function
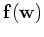 , as a linear function of
, as a linear function of 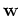 ,
is also a zero-mean Gaussian:
,
is also a zero-mean Gaussian:
where
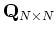 is the covariancee matrix of
is the covariancee matrix of 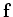 :
:
with the mn-th component being:
In particular, when
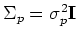 , we get
, we get
The function 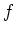 is a Gaussian process as the distribution
is a Gaussian process as the distribution
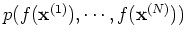 of any
of any 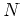 of its
values correponding to
of its
values correponding to 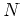 input points is a Gaussian. As the noise
input points is a Gaussian. As the noise
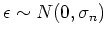 is also a Gaussian distribution, the
distribution of the
is also a Gaussian distribution, the
distribution of the 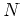 values of the output
values of the output
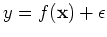 are also Gaussian:
are also Gaussian:
where
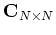 is the covariance matrix of
is the covariance matrix of 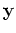 :
:
with the mn-th component being:
The result above can be generalized when
 , i.e.,
the function
, i.e.,
the function 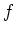 is expressed as the linear combination (integration
rather than summation) of basis functions. For example, assume
is expressed as the linear combination (integration
rather than summation) of basis functions. For example, assume 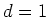 and the h-th basis is a radial function centered at
and the h-th basis is a radial function centered at 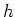 :
:
and
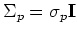 , the covariance
, the covariance 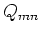 becomes
becomes
where 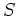 and
and 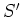 are some scaling factors (including
are some scaling factors (including 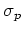 ).
More generally, when
).
More generally, when 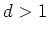 ,
the covariance matrix of the
,
the covariance matrix of the 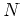 function values
function values 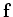 at the
at the 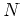 input points
input points
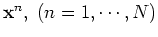 can be defined as
can be defined as
Now the regression problem can be approached based on a totally different
point of view. Instead of specifying the basis functions and some model
parameters (e.g. the weights 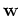 ), we can assume the
), we can assume the 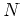 function
values
function
values 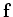 to be a Gaussian process and construct its covariance
matrix (while always assume zeromean vector):
to be a Gaussian process and construct its covariance
matrix (while always assume zeromean vector):
The mn-th component of the covariance matrix is
which be constructed according to the specific problem. For example, the
following covariances can be used:
Comments:
- The motivation behind the general form of these covarances is the
intuition that similar inputs (small
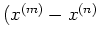 ) should give rise
to similar predictions (large covarance or correlation
) should give rise
to similar predictions (large covarance or correlation  ).
).
- Here the covarance
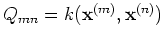 can be
considered as some kernel function of the two vector arguments as used
in various kernel-based algorithms such as support vector machine and
kernel PCA. In either case, these kernels need to be constructed based
on some prior knowledge of the problem.
can be
considered as some kernel function of the two vector arguments as used
in various kernel-based algorithms such as support vector machine and
kernel PCA. In either case, these kernels need to be constructed based
on some prior knowledge of the problem.
For the output
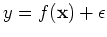 , the covariance matrix becomes:
, the covariance matrix becomes:
and its prior distribution is:
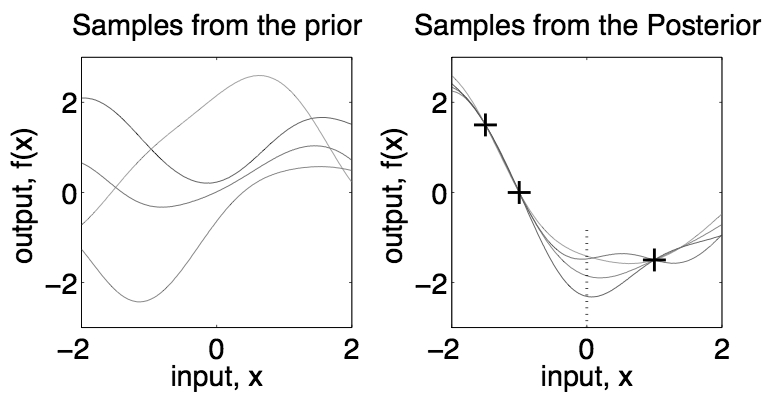
Samples from this distribution 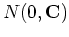 can be drawn to get the
can be drawn to get the 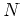 values of the function
values of the function 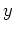 , i.e., various curves in 1-D space.
, i.e., various curves in 1-D space.
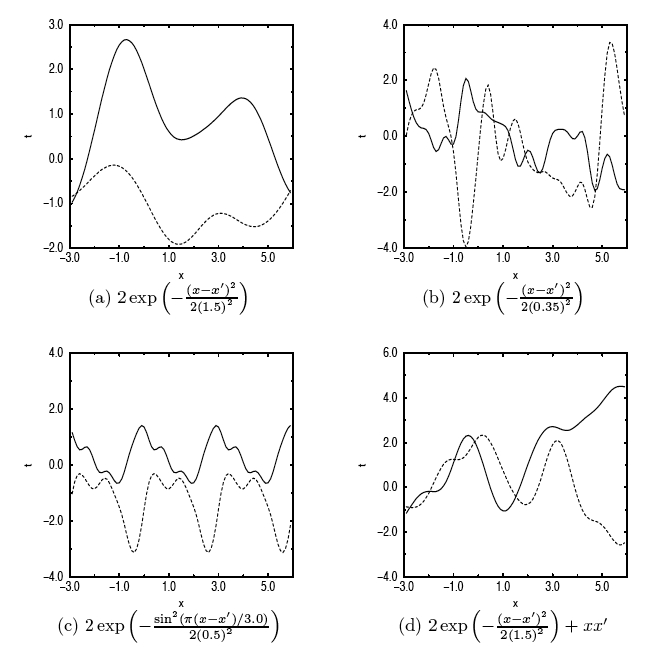
Now the regression problem of finding the underlying function 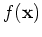 to fit the observed data
to fit the observed data
is turned into a problem of finding the posterior distribution of the
output:
As the function 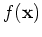 as well as output
as well as output
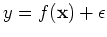 are
Gaussian process, the conditional distribution of
are
Gaussian process, the conditional distribution of 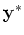 given
given 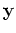 can be found as below (proof given in Appendix A).
can be found as below (proof given in Appendix A).
We first consider finding the conditional distribution of function values
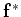 . Set up the function vector containing both the known values
. Set up the function vector containing both the known values
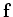 and the prediction
and the prediction 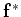 :
:
The normal distribution of this vector is determined by the mean vector
(assumed to be zero) and the constructed covariance matrix, which is
expressed in four blocks according to the dimensions (number of points)
of 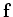 and
and 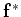 :
:
Now the conditional distribution of 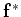 given
given 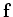 can be
found:
can be
found:
where
As the covariance matrix
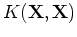 is symmetric,
is symmetric,
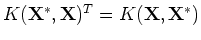 .
.
If 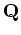 above is replaced by
above is replaced by
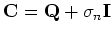 , the
discussion is also valid for output
, the
discussion is also valid for output 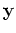 .
.
The samples drawn from this posterior distribution
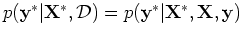 are different curves that interpolate (fit) the observed data, the
are different curves that interpolate (fit) the observed data, the 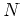 data points
data points
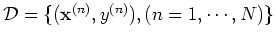 , and
they can also predict the outputs
, and
they can also predict the outputs 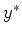 at any input points
at any input points 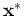 .
.
In summary, the regression problem can be approached in two different ways:
These two views can be unified by the Mercer's theorem: a given positive
definite covariance function can be decomposed as
where 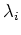 and
and 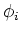 are the eigenvalues and eigenfunctions
respectively:
are the eigenvalues and eigenfunctions
respectively:
In the weight space view, the covariance matrix is a result of the
basis functions and their weights, while in the function space view, the
covariance matrix is constructed first without explicitely specifying the
basis functions and their weight.



Next: Appendix A: Conditional and
Up: Gaussiaon Process
Previous: Nonlinar Regression
Ruye Wang
2006-11-14
![]() can be written as
can be written as
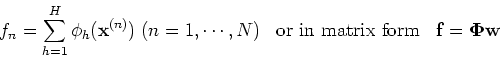
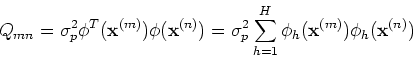
![]() is a Gaussian process as the distribution
is a Gaussian process as the distribution
![]() of any
of any ![]() of its
values correponding to
of its
values correponding to ![]() input points is a Gaussian. As the noise
input points is a Gaussian. As the noise
![]() is also a Gaussian distribution, the
distribution of the
is also a Gaussian distribution, the
distribution of the ![]() values of the output
values of the output
![]() are also Gaussian:
are also Gaussian:
![]() , i.e.,
the function
, i.e.,
the function ![]() is expressed as the linear combination (integration
rather than summation) of basis functions. For example, assume
is expressed as the linear combination (integration
rather than summation) of basis functions. For example, assume ![]() and the h-th basis is a radial function centered at
and the h-th basis is a radial function centered at ![]() :
:
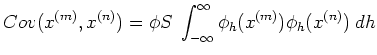
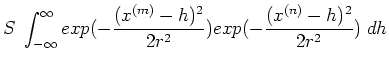
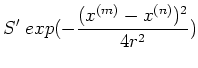
![]() ), we can assume the
), we can assume the ![]() function
values
function
values ![]() to be a Gaussian process and construct its covariance
matrix (while always assume zeromean vector):
to be a Gaussian process and construct its covariance
matrix (while always assume zeromean vector):
![\begin{displaymath}\Sigma_f={\bf Q}=Cov({\bf f})=\left[ \begin{array}{ccc}...&.....
......&...&...\end{array} \right]_{N\times N}
=K({\bf X},{\bf X}) \end{displaymath}](img91.png)
![]() , the covariance matrix becomes:
, the covariance matrix becomes:

![]() to fit the observed data
to fit the observed data
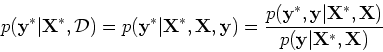
![]() . Set up the function vector containing both the known values
. Set up the function vector containing both the known values
![]() and the prediction
and the prediction ![]() :
:
![\begin{displaymath}\Sigma_f=Cov\left[ \begin{array}{c} {\bf f} {\bf f}^* \end...
...\bf X}^*,{\bf X}) & K({\bf X}^*,{\bf X}^*) \end{array} \right] \end{displaymath}](img108.png)
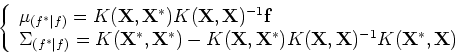
![]() above is replaced by
above is replaced by
![]() , the
discussion is also valid for output
, the
discussion is also valid for output ![]() .
.
![]() are different curves that interpolate (fit) the observed data, the
are different curves that interpolate (fit) the observed data, the ![]() data points
data points
![]() , and
they can also predict the outputs
, and
they can also predict the outputs ![]() at any input points
at any input points ![]() .
.