


Next: Gaussian process
Up: Gaussiaon Process
Previous: Linar Regression
To enhance the expressive power of the linear regression model
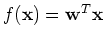 , it can be generalized to a nonlinear model
based on a set of
, it can be generalized to a nonlinear model
based on a set of 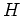 basis functions
basis functions
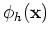 (
(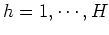 ):
):
where
The dimensionality of the weight vector 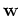 has changed from
has changed from
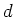 (dimensionality of
(dimensionality of 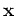 ) to
) to 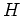 (number of basis functions).
(number of basis functions).
For example, when the dimensionality of 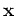 is
is 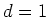 ,the basis
function can be
,the basis
function can be
each centered around some point 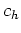 . Alternatively, the basis functions
of a scalar
. Alternatively, the basis functions
of a scalar 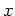 can be
can be
In such cases, the previous derivation is still valid if we replace 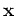 by
by
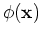 and the predictive distribution is
and the predictive distribution is
where
where
with each column for each of the 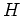 basis functions
basis functions
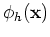 containing the
containing the 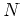 function values at the
function values at the 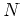 input data points
input data points
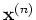 (
(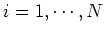 ):
):
Ruye Wang
2006-11-14
![]() , it can be generalized to a nonlinear model
based on a set of
, it can be generalized to a nonlinear model
based on a set of ![]() basis functions
basis functions
![]() (
(![]() ):
):
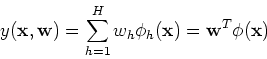
![]() is
is ![]() ,the basis
function can be
,the basis
function can be
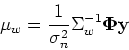
![\begin{displaymath}{\bf\Phi}({\bf X})=[ {\bf\phi}_1({\bf X}),\cdots,{\bf\phi}_H(...
... ... & \phi_H({\bf x}^{(N)})
\end{array} \right]_{N\times H} \end{displaymath}](img55.png)