


Next: Two-Dimensional Fourier Transform (2DFT)
Up: fourier
Previous: Fast Fourier Transform (FFT)
First we recall the symmetry properties of the DFT. The DFT of
![$x[m]=x_r[m]+jx_i[m]$](img146.png) is defined as
is defined as
where ![$X_r[n]$](img151.png) and
and ![$X_i[n]$](img152.png) are the real and imaginary part of the spectrum
respectively.
If
are the real and imaginary part of the spectrum
respectively.
If ![$x[m]$](img8.png) is real, i.e.,
is real, i.e.,
![$x_i[m] \equiv 0$](img153.png) , then we have
, then we have
or
If ![$x[m]$](img8.png) is imaginary, i.e.,
is imaginary, i.e.,
![$x_r[m] \equiv 0$](img156.png) , then we have
, then we have
or
Next we show how an arbitrary function 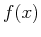 can be decomposed into the even
and odd components
can be decomposed into the even
and odd components 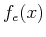 and
and 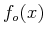 :
:
and
Now we are ready to show how to Fourier transform two real functions ![$x_1[m]$](img164.png) and
and 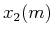 to get their spectra
to get their spectra ![$X_1[n]$](img166.png) and
and ![$X_2[n]$](img167.png) by one DFT.
by one DFT.
- Define a complex function
![$x[m]$](img8.png) by the two real functions:
by the two real functions:
Notice here that we impose 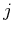 on
on ![$x_2[m]$](img170.png) to make it imaginary.
to make it imaginary.
- Find the DFT of
![$x[m]$](img8.png)
- Separate
![$X[n]$](img19.png) into
into ![$X_1[n]$](img166.png) and
and ![$X_2[n]$](img167.png) , the spectra of
, the spectra of ![$x_1[m]$](img164.png) and
and ![$x_2[m]$](img170.png) , using the symmetry properties discussed previously.
Note that
, using the symmetry properties discussed previously.
Note that ![$X[-n]=X[N-n]$](img177.png) because
because ![$X[n]$](img19.png) is a periodic function.
is a periodic function.



Next: Two-Dimensional Fourier Transform (2DFT)
Up: fourier
Previous: Fast Fourier Transform (FFT)
Ruye Wang
2009-12-31
![$\displaystyle \sum_{m=0}^{N-1} x[m]e^{-j2\pi mn/N}=\sum_{m=0}^{N-1} [x_r[m]+jx_i[m]]
[cos(2\pi mn/N)-j\;sin(2\pi mn/N)]$](img148.png)
![$\displaystyle \sum_{m=0}^{N-1} [x_r[m]cos(\frac{2\pi mn}{N})+x_i[m]sin(\frac{2\...
...
+j\sum_{m=0}^{N-1} [x_i[m]cos(\frac{2\pi mn}{N})-x_r[m]sin(\frac{2\pi mn}{N})]$](img149.png)
![$\displaystyle \sum_{m=0}^{N-1} x[m]e^{-j2\pi mn/N}=\sum_{m=0}^{N-1} [x_r[m]+jx_i[m]]
[cos(2\pi mn/N)-j\;sin(2\pi mn/N)]$](img148.png)
![$\displaystyle \sum_{m=0}^{N-1} [x_r[m]cos(\frac{2\pi mn}{N})+x_i[m]sin(\frac{2\...
...
+j\sum_{m=0}^{N-1} [x_i[m]cos(\frac{2\pi mn}{N})-x_r[m]sin(\frac{2\pi mn}{N})]$](img149.png)
![\begin{displaymath}\left\{ \begin{array}{c} X_r[-n]=X_r[n] X_i[-n]=-X_i[n] \end{array} \right.
\end{displaymath}](img154.png)
![\begin{displaymath}\left\{ \begin{array}{c} X_r[-n]=-X_r[n] X_i[-n]=X_i[n] \end{array} \right.
\end{displaymath}](img157.png)
![]() can be decomposed into the even
and odd components
can be decomposed into the even
and odd components ![]() and
and ![]() :
:
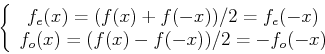
![]() and
and ![]() to get their spectra
to get their spectra ![]() and
and ![]() by one DFT.
by one DFT.