


Next: A 2D DFT Example
Up: fourier
Previous: Physical Meaning of 2DFT
Reconsider the 2D DFT:
where
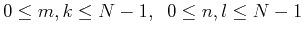 and
and
As the summation above is with respect to the row index 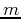 and the column index
and the column index
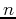 can be treated as a fixed parameter, this expression can be considered as a
one-dimensional Fourier transform of the nth column of
can be treated as a fixed parameter, this expression can be considered as a
one-dimensional Fourier transform of the nth column of ![$[x]$](img262.png) (
(
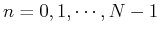 ),
which can be written in column vector (vertical) form as:
),
which can be written in column vector (vertical) form as:
for all columns
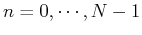 . Putting all these
. Putting all these 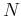 columns together, we can write
columns together, we can write
or more concisely
where 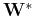 is a
is a 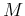 by
by 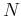 Fourier transform matrix.
Fourier transform matrix.
We also note that the summation in the expression for ![$X[k,l]$](img207.png) is with respective
to the column index n and the row index number k can be treated as a fixed
parameter, the expression is one-dimensional Fourier transform of the kth row of
is with respective
to the column index n and the row index number k can be treated as a fixed
parameter, the expression is one-dimensional Fourier transform of the kth row of
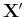 , which can be written in row vector (horizontal) form as
, which can be written in row vector (horizontal) form as
Putting all these 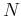 rows together, we can write
rows together, we can write
(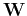 is symmetric:
is symmetric:
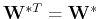 ), or more concisely
), or more concisely
But since
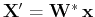 , we have
, we have
This transform expression indicates that 2D DFT can be implemented by transforming
all the rows of  and then transforming all the columns of the resulting
matrix. The order of the row and column transforms is not important.
and then transforming all the columns of the resulting
matrix. The order of the row and column transforms is not important.
Similarly, the inverse 2D DFT can be written as
Again note that 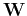 is a symmetric Unitary matrix:
is a symmetric Unitary matrix:
It is obvious that the complexity of 2D DFT is 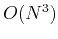 which can be
reduced to
which can be
reduced to
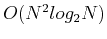 if FFT is used.
if FFT is used.



Next: A 2D DFT Example
Up: fourier
Previous: Physical Meaning of 2DFT
Ruye Wang
2009-12-31
![\begin{displaymath}
X[k,l] = \frac{1}{\sqrt{MN}}\sum_{n=0}^{N-1} [ \sum_{m=0}^{...
... X'[k,n] e^{-j2\pi \frac{nl}{N} }
\;\;\;\;(k=0,1,\cdots,M-1)
\end{displaymath}](img258.png)
![\begin{displaymath}
X[k,l] = \frac{1}{\sqrt{MN}}\sum_{n=0}^{N-1} [ \sum_{m=0}^{...
... X'[k,n] e^{-j2\pi \frac{nl}{N} }
\;\;\;\;(k=0,1,\cdots,M-1)
\end{displaymath}](img258.png)
![\begin{displaymath}X'[k,n]\stackrel{\triangle}{=}\frac{1}{\sqrt{M}}\sum_{m=0}^{N-1}x[m,n]e^{-j2\pi \frac{mk}{M}} \;\;\;\;\;(n=0,1,\cdots,N-1) \end{displaymath}](img260.png)
![]() is with respective
to the column index n and the row index number k can be treated as a fixed
parameter, the expression is one-dimensional Fourier transform of the kth row of
is with respective
to the column index n and the row index number k can be treated as a fixed
parameter, the expression is one-dimensional Fourier transform of the kth row of
![]() , which can be written in row vector (horizontal) form as
, which can be written in row vector (horizontal) form as
![\begin{displaymath}\left[ \begin{array}{c}
{\bf X}_0^T . . {\bf X}_{N-1}...
...^T . . {\bf X}'_{N-1}^T \end{array} \right]
{\bf W}^*
\end{displaymath}](img271.png)
![]() which can be
reduced to
which can be
reduced to
![]() if FFT is used.
if FFT is used.