Consider the Fourier transform of continuous but non-periodic signal (the
result should be easily generalized to other cases):
The complex exponential is composed of two sinusoidal functions:
![]() .
First we define the following:
.
First we define the following:
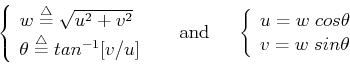
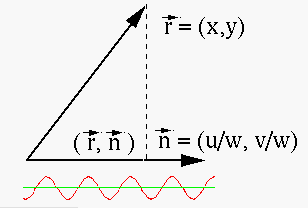
The complex coefficient
![]() can also be represented
in polar form in terms of its amplitude and phase:
can also be represented
in polar form in terms of its amplitude and phase:
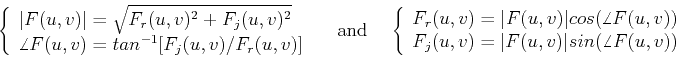
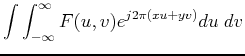 |
|||
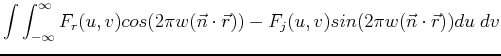 |
|||
![$\displaystyle \int \int_{-\infty}^{\infty} \vert F(u,v)\vert
[ cos\angle F(u,v)...
...n} \cdot \vec{r}))
-sin\angle F(u,v) sin(2\pi w(\vec{n} \cdot \vec{r})) ]du\;dv$](img233.png) |
|||
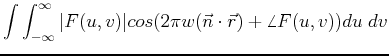 |
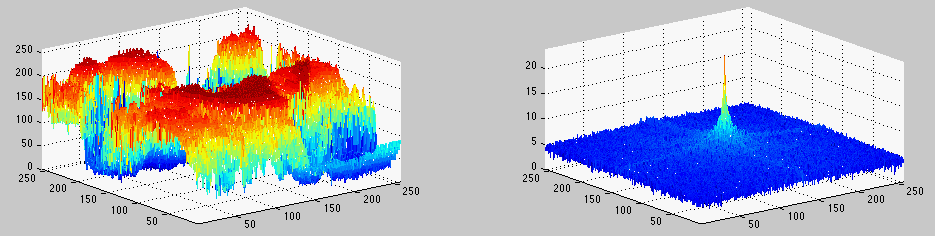
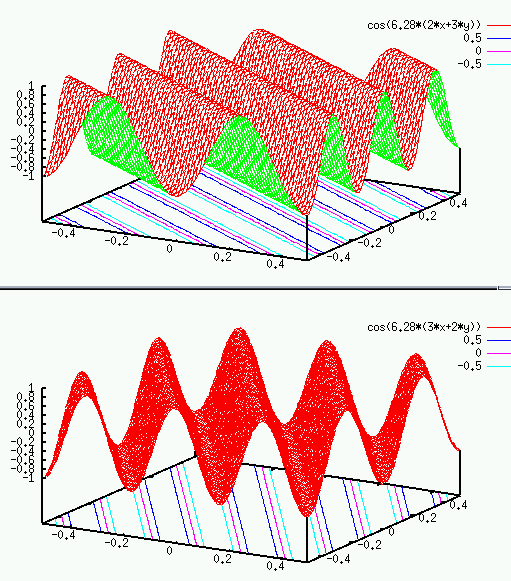
Example 0
The 2D function shown below has three frequency components (2D sinusoidal waves) of different directions:
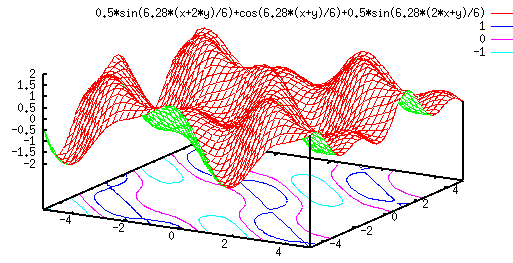
Example 1
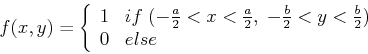
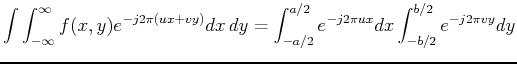 |
|||
 |
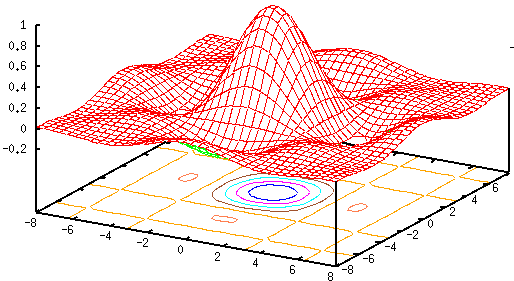
Example 2
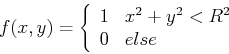
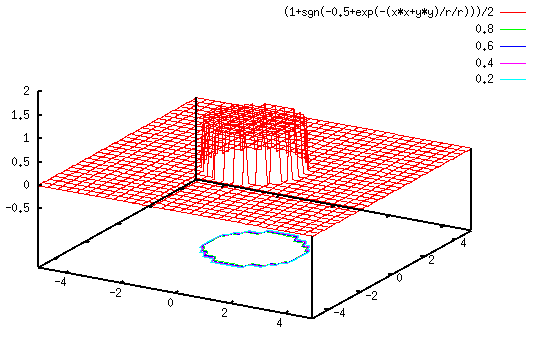
It is more convenient to use polar coordinate system in both spatial and frequency domains. Let

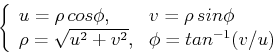
we have:
![$\displaystyle \int \int_{-\infty}^{\infty} f(x,y) e^{-j2\pi(ux+vy)} dx dy
= \i...
...\pi} e^{-j2\pi r\rho(cos \theta cos \phi
+ sin \theta sin \phi)} d\theta ] r dr$](img247.png) |
|||
![$\displaystyle \int_0^R [ \int_0^{2\pi} e^{-j2\pi r\rho cos (\theta-\phi)}
d\theta ] r dr
= \int_0^R [ \int_0^{2\pi} e^{-j2\pi r\rho cos \theta}
d\theta ] r dr$](img248.png) |
To continue, we need to use 0th order Bessel function ![]() defined as
defined as
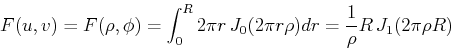
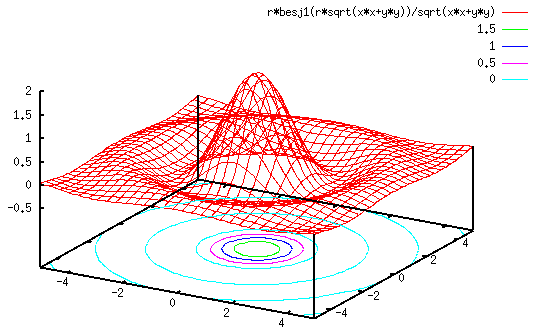
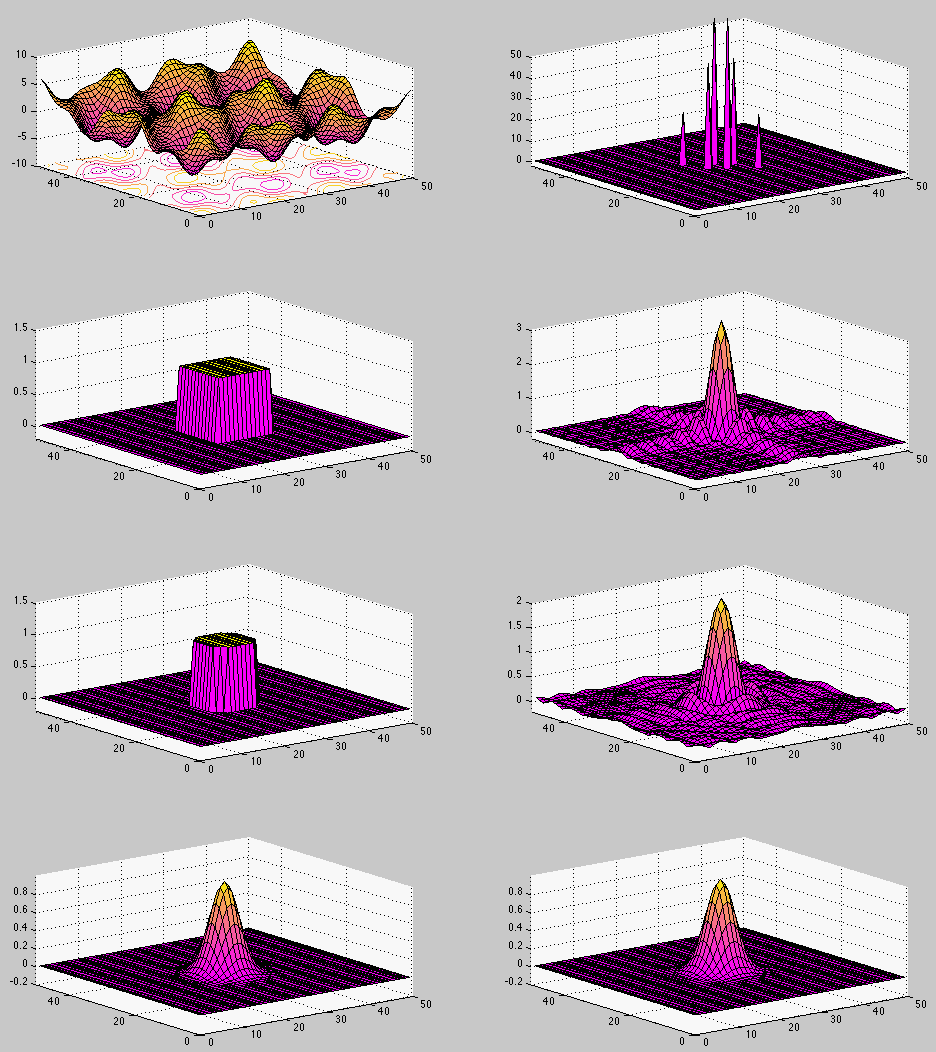
Example 3 2D DFT of an image: