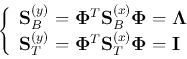Next: Information conservation in feature
Up: Feature Selection
Previous: Optimal transformation for maximizing
The previous method only maximizes the between-class scatteredness 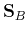 without taking into consideration the within-class scatteredness
without taking into consideration the within-class scatteredness 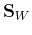 ,
or, equivalently, the total scatteredness
,
or, equivalently, the total scatteredness
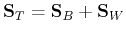 . As
it is possible that in the space after the transform
. As
it is possible that in the space after the transform
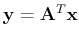 the between-class scatteredness
the between-class scatteredness
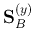 is maximized but so is the
total scatteredness
is maximized but so is the
total scatteredness
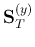 , while it is desirable to maximize
, while it is desirable to maximize
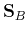 and minimize
and minimize 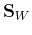 at the same time in order to maximize
the separability. We therefore choose
at the same time in order to maximize
the separability. We therefore choose
![$J=tr[{\bf S}_W^{-1}{\bf S}_B]$](img58.png) as a
better criterion for feature selection.
as a
better criterion for feature selection.
In order to find the optimal transform matrix
![${\bf A}=[{\bf a}_1,\cdots,{\bf a}_M]$](img59.png) ,
we consider the maximization of the objective function
,
we consider the maximization of the objective function 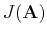 :
:
where
and
Note that as
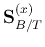 here is not symmetric (the product of two
symmetric matrices is in general not symmetric), the method used for the
maximization of
here is not symmetric (the product of two
symmetric matrices is in general not symmetric), the method used for the
maximization of
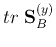 considered previously can no longer be
used to maximize
considered previously can no longer be
used to maximize
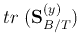 .
.
To address the problem of maximization of 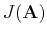 , we first consider
the case of
, we first consider
the case of  , i.e.,
, i.e.,
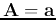 , to find a single feature
, to find a single feature
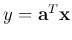 . The objective function
. The objective function 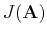 above becomes
above becomes
This function of 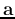 is the
Rayleigh quotient
is the
Rayleigh quotient
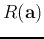 of the two symmetric matrices
of the two symmetric matrices
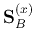 and
and
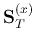 . The optimal
transform vector
. The optimal
transform vector 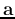 that maximizes
that maximizes  can be found by solving
the corresponding
generalized eigenvalue problem
can be found by solving
the corresponding
generalized eigenvalue problem
where 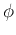 is an eigenvector of
is an eigenvector of
![${\bf S}_{B/T}=[{\bf S}_T^{(x)}]^{-1}{\bf S}_B^{(x)}$](img79.png) ,
and the corresponding eigenvalue is
,
and the corresponding eigenvalue is
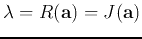 , which is
maximized by the eigenvector
, which is
maximized by the eigenvector 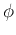 corresponding to the greatest eigenvalue
corresponding to the greatest eigenvalue
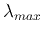 .
.
Next, we generalize this approach the case of 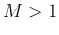 , by solving the generalized
eigen-equation
, by solving the generalized
eigen-equation
where the eigenvector matrix
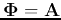 is used as the linear
transform matrix by which both
is used as the linear
transform matrix by which both
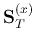 and
and
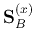 can be
diagonalized at the same time:
can be
diagonalized at the same time:
We see that the signal components in 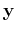 are completely decorrelated,
i.e., they each carry some separability information independent of others.
We can therefore construct the transform matrix
are completely decorrelated,
i.e., they each carry some separability information independent of others.
We can therefore construct the transform matrix
![${\bf\Phi}_{N\times M}=[{\bf\phi}_1,
\cdots,{\bf\phi}_M]$](img86.png) composed of the
composed of the 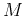 eigenvectors corresponding to the
eigenvectors corresponding to the 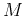 largest eigenvalues, for the Rayleigh quotient
largest eigenvalues, for the Rayleigh quotient
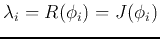 representing the separability in the ith dimension for
representing the separability in the ith dimension for
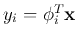 ,
(
,
(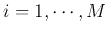 ).
).
The generalized eigen-equation above can be further written as
where 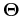 is a diagonal matrix composed of
is a diagonal matrix composed of
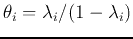 on its diagonal:
on its diagonal:
We see that using the 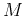 greatest eigenvalues
greatest eigenvalues 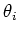 of
of 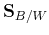 to
maximize
to
maximize 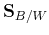 is equivalent to using the
is equivalent to using the 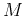 greatest eigenvalues
greatest eigenvalues
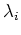 of
of 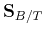 to maximize
to maximize 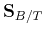 .
.



Next: Information conservation in feature
Up: Feature Selection
Previous: Optimal transformation for maximizing
Ruye Wang
2017-03-30
![]() without taking into consideration the within-class scatteredness
without taking into consideration the within-class scatteredness ![]() ,
or, equivalently, the total scatteredness
,
or, equivalently, the total scatteredness
![]() . As
it is possible that in the space after the transform
. As
it is possible that in the space after the transform
![]() the between-class scatteredness
the between-class scatteredness
![]() is maximized but so is the
total scatteredness
is maximized but so is the
total scatteredness
![]() , while it is desirable to maximize
, while it is desirable to maximize
![]() and minimize
and minimize ![]() at the same time in order to maximize
the separability. We therefore choose
at the same time in order to maximize
the separability. We therefore choose
![]() as a
better criterion for feature selection.
as a
better criterion for feature selection.
![]() ,
we consider the maximization of the objective function
,
we consider the maximization of the objective function ![]() :
:
![]() , we first consider
the case of
, we first consider
the case of ![]() , i.e.,
, i.e.,
![]() , to find a single feature
, to find a single feature
![]() . The objective function
. The objective function ![]() above becomes
above becomes
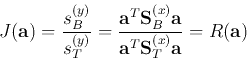
![]() , by solving the generalized
eigen-equation
, by solving the generalized
eigen-equation