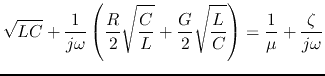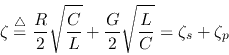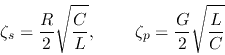Next: Reflection and termination
Up: transmission_line
Previous: transmission_line
As shown in the figure, a transmission line can be modeled by its
resistance and inductance in series, and the conductance and capacitance
in parallel, all distributed along its length in  direction. Here
direction. Here 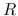 ,
,
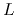 ,
, 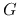 and
and 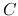 represent, respectively, the resistance, inductance,
conductance, and capacitance per unit length
(
represent, respectively, the resistance, inductance,
conductance, and capacitance per unit length
(
![$[ohm]/[meter],\;[siemens]/[meter],\;[henry]/[meter],\;[farad]/[meter] $](img6.png) ).
).

The voltage 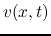 and current
and current 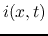 along the transmission line are
functions of both time variable
along the transmission line are
functions of both time variable 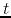 and space variable
and space variable 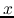 . Across an
infinitesimal section
. Across an
infinitesimal section 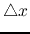 along the line, the voltage and current
changes are
along the line, the voltage and current
changes are
Dividing both sides of these equations by 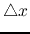 and let
and let
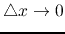 we get the telegrapher's equations:
we get the telegrapher's equations:
These coupled partial differential equations (PDEs) of two variables 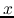 and
and
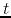 , called the telegrapher's equations, can be more conveniently solved by
the Fourier transform method. We denote the Fourier transforms of the voltage
and current with respect of
, called the telegrapher's equations, can be more conveniently solved by
the Fourier transform method. We denote the Fourier transforms of the voltage
and current with respect of 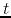 (
(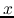 treated as a parameter) as
treated as a parameter) as
For convenience we may sometimes denote the voltage 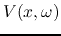 and current
and current
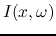 in the Fourier domain as
in the Fourier domain as 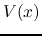 and
and 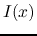 or simply
or simply 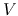 and
and 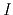 .
Taking the Fourier transform on both sides of the two PDEs we get two ordinary
differential equations (ODEs) with respect to a single variable
.
Taking the Fourier transform on both sides of the two PDEs we get two ordinary
differential equations (ODEs) with respect to a single variable 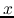 :
:
These ODEs can also be obtained when both voltage 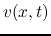 and current
and current 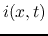 are represented respectively as phasors
are represented respectively as phasors 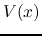 and
and 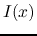 , and the transmission
line is represented in terms of the impedances
, and the transmission
line is represented in terms of the impedances 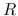 ,
, 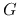 ,
, 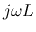 , and
, and
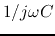 . Therefore the variables
. Therefore the variables 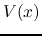 and
and 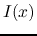 in the ODEs can be
considered as either the Fourier transform or the phasor representations of
the voltage
in the ODEs can be
considered as either the Fourier transform or the phasor representations of
the voltage 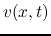 and current
and current 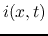 .
.
Combining the two equations we get
where we have defined
with
and
The solutions of these two second order ODEs can be found to be:
where we have defined
Here 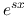 and
and 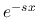 are the two particular solutions, weighted by
the arbitrary constants
are the two particular solutions, weighted by
the arbitrary constants 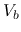 and
and 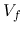 , which are to be determined based
on the boundary conditions
, which are to be determined based
on the boundary conditions
![$V(0)={\cal F}[v(0,t)]$](img34.png) at the front and
at the front and
![$V(l)={\cal F}[v(l,t)]$](img35.png) at the back end of the transmission line of length
at the back end of the transmission line of length
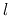 . Note that
. Note that 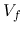 and
and 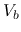 are constants with respect to variable
are constants with respect to variable 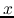 ,
but in time domain, they are still functions of variable
,
but in time domain, they are still functions of variable 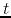 . Constant
. Constant 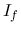 and
and 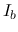 can be found the same way.
can be found the same way.
Substituting
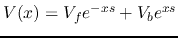 into the equation
into the equation
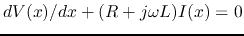 and solving for
and solving for 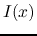 , we get
, we get
where
is the characteristic impedance of the transmission line measured in ohm.
Comparing the two expressions of 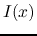 above, we see that
above, we see that
Lossless transmission line
When the frequency 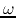 is high,
is high, 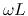 and
and 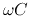 are much
greater than
are much
greater than 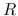 and
and 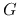 , we can assume the transmission line is loss-less
with
, we can assume the transmission line is loss-less
with 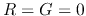 . In this case the two ODEs above become
. In this case the two ODEs above become
and we also have
where 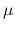 the transmission speed (measued in meter/second) defined as
the transmission speed (measued in meter/second) defined as
and
The voltage and current in time domain can be obtained as the inverse Fourier
transforms of
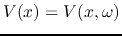 and
and
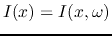 :
:
and
where
Both 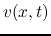 and
and 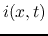 are composed of two components traveling at velocity
are composed of two components traveling at velocity
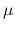 in opposite directions along the transmission line. The time for the wave
to travel the whole length
in opposite directions along the transmission line. The time for the wave
to travel the whole length 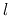 of the transmission line is
of the transmission line is 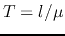 . At the
front (
. At the
front (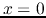 ) and back (
) and back (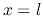 ) ends of the line we have
) ends of the line we have
i.e., the coefficients 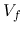 and
and 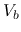 are just the forward and backward
voltages at the front of the line (
are just the forward and backward
voltages at the front of the line (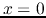 ):
):
Lossy transmission line
When the signal frequency is low, 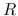 and
and 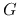 can no longer be assumed as
zero and the signal is always attenuated due to the resistance
can no longer be assumed as
zero and the signal is always attenuated due to the resistance 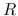 in serie
with the inductance
in serie
with the inductance 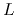 and the leakage conductance
and the leakage conductance 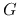 in parallel with the
capacitance
in parallel with the
capacitance 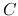 . The two first order ODEs can be written as
. The two first order ODEs can be written as
where we have defined
As the above equations take the same form as in the loss-less case (with 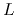 and
and 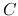 replaced by
replaced by 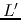 and
and 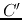 , respectively), it can be solved in the
same way. Now we have
, respectively), it can be solved in the
same way. Now we have
and
which can be approximated as below when 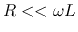 ,
, 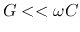 :
:
The second approximation is due to the Taylor series:
Here we have defined the attenuation constant or damping coefficient
as
which is simply the sum of the damping coefficient 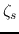 of the
series RCL circuit and the damping coefficient
of the
series RCL circuit and the damping coefficient 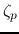 of the parallel
GCL circuit:
of the parallel
GCL circuit:
As before, the solution of the above equations is
In the time domain we have
Note that the forward wave 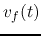 attenuates exponentially as
attenuates exponentially as 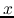 increases
from 0 to
increases
from 0 to 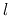 , while the backward wave
, while the backward wave 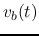 attenuates exponentially as
attenuates exponentially as 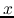 decreases from
decreases from 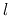 to 0.
to 0.



Next: Reflection and termination
Up: transmission_line
Previous: transmission_line
Ruye Wang
2016-05-20
![]() direction. Here
direction. Here ![]() ,
,
![]() ,
, ![]() and
and ![]() represent, respectively, the resistance, inductance,
conductance, and capacitance per unit length
(
represent, respectively, the resistance, inductance,
conductance, and capacitance per unit length
(
![]() ).
).

![]() and current
and current ![]() along the transmission line are
functions of both time variable
along the transmission line are
functions of both time variable ![]() and space variable
and space variable ![]() . Across an
infinitesimal section
. Across an
infinitesimal section ![]() along the line, the voltage and current
changes are
along the line, the voltage and current
changes are
![]() into the equation
into the equation
![]() and solving for
and solving for ![]() , we get
, we get
![\begin{displaymath}I(x)=-\frac{1}{j\omega L+R}\frac{dV(x)}{dx}
=\frac{s}{(j\ome...
... e^{-xs}-V_b e^{xs}]
=\frac{1}{Z_0}\;[V_f e^{-xs}-V_b e^{xs}]
\end{displaymath}](img41.png)
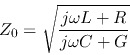
![]() is high,
is high, ![]() and
and ![]() are much
greater than
are much
greater than ![]() and
and ![]() , we can assume the transmission line is loss-less
with
, we can assume the transmission line is loss-less
with ![]() . In this case the two ODEs above become
. In this case the two ODEs above become
![]() and
and ![]() can no longer be assumed as
zero and the signal is always attenuated due to the resistance
can no longer be assumed as
zero and the signal is always attenuated due to the resistance ![]() in serie
with the inductance
in serie
with the inductance ![]() and the leakage conductance
and the leakage conductance ![]() in parallel with the
capacitance
in parallel with the
capacitance ![]() . The two first order ODEs can be written as
. The two first order ODEs can be written as
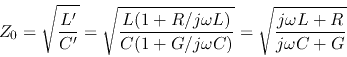
![\begin{displaymath}\sqrt{L'C'}=\sqrt{LC}\left[ \left(1+\frac{R}{j\omega L}\right)
\left(1+\frac{G}{j\omega C}\right) \right]^{1/2} \end{displaymath}](img71.png)
![$\displaystyle \sqrt{LC}\left(1+\frac{R}{j\omega L}+\frac{G}{j\omega C}\right)^{...
...}\left[1+\frac{1}{2}\left(\frac{R}{j\omega L}+\frac{G}{j\omega C}\right)\right]$](img76.png)