Algebraic Summer

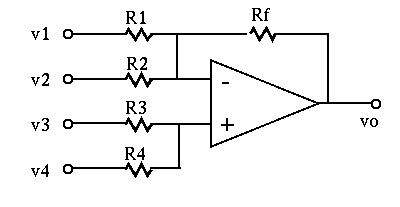
Define $V\stackrel{\triangle}{=}V^+ \approx V^-$ . Apply KCL to $V^-$ and $V^+$ we get:

$\displaystyle \frac{V_1-V}{R_1}+\frac{V_2-V}{R_2}+\frac{V_{out}-V}{R_f}=0,\;\;\;\;\;\;$ and $\displaystyle \;\;\;\;\;\;\;\; \frac{V_3-V}{R_3}+\frac{V_4-V}{R_4}=0$

(1)

Solving the 2nd equation for $V$

we get:

$\displaystyle V=\frac{R_4}{R_3+R_4} V_3 + \frac{R_3}{R_3+R_4} V_4$

(2)

and substitute it into the first equation to get

$\displaystyle V_{out}=-\frac{R_f}{R_1}V_1-\frac{R_f}{R_2}V_2 +\left(\frac{R_f}{... ...R_f}{R_2}+1\right) \left(\frac{R_4}{R_3+R_4} V_3+\frac{R_3}{R_3+R_4} v_4\right)$

(3)

We see that the output is some algebraic sum of the inputs with both positive and negative coefficients.

In general, if there are $m$ inputs to the inverting side and $n$ inputs to the non-inverting side, then we have

$\displaystyle \sum_{i=1}^m\frac{V_i-V}{R_i}=\frac{V-V_{out}}{R_f}$

(4)

and

$\displaystyle \sum_{j=1}^n\frac{V_j-V}{R_j}=\sum_{j=1}^n\frac{V_j}{R_j} -\left(\sum_{j=1}^n\frac{1}{R_j}V\right) =0$

(5)

Solving for $V$

we get

$\displaystyle V=\frac{\sum_{j=1}^nV_j/R_j}{\sum_{j=1}^n1/R_j}$

(6)

Substituting this into the first equation and solving for $V_{out}$ we get

$\displaystyle V_{out}=-\sum_{i=1}^m \frac{R_f}{R_i}V_i +\left(\sum_{i=1}^m\frac{R_f}{R_i}+1\right) \frac{\sum_{j=1}^nV_j/R_j}{\sum_{j=1}^n 1/R_j}=\sum_i k_iV_i$

(7)