Next: Analysis of Op-Amp Circuits Up: Chapter 5: Operational Amplifiers Previous: Chapter 5: Operational Amplifiers
The circuit schematic of the typical 741 op-amp is shown below:
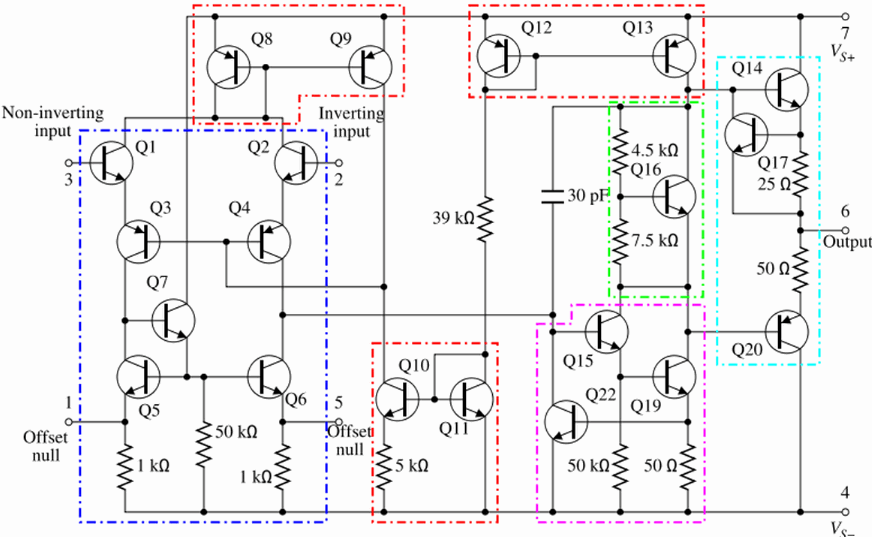
A component-level diagram of the common 741 op-amp. Dotted lines outline:
Like all op-amps, the circuit basically consists of three stages:
 .
.
 of both polarities
(typically
of both polarities
(typically  V).
V).
Although the op-amp circuit may look complicated, the analysis of its operation and behaviors can be simplfied based on the following assumptions:
 can be treated as infinity
can be treated as infinity
 .
.
 ),
and could be approximated to be zero
),
and could be approximated to be zero  .
.
 can be treated as zero
can be treated as zero
 ,
i.e., the output
,
i.e., the output  is not affected by the load
is not affected by the load  (so long as it is
much greater than
(so long as it is
much greater than  ).
).
 ), i.e., the property of the op-amp
remain unchanged for all frequencies of interest.
), i.e., the property of the op-amp
remain unchanged for all frequencies of interest.
Based on these approximations, an op-amp can be modeled in terms of the following three parameters:
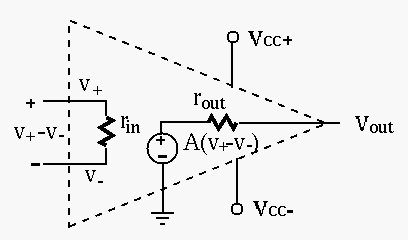
 : very large, typically a few mega-Ohms or
higher (
: very large, typically a few mega-Ohms or
higher (
 , e.g., 741
, e.g., 741
 ), depending on
the frequency and specific components used (e.g., BJT or FET).
), depending on
the frequency and specific components used (e.g., BJT or FET).
 :, very small, typically a few tens of
ohms, e.g., 75
:, very small, typically a few tens of
ohms, e.g., 75  .
.
 :, based on both the inverting input
:, based on both the inverting input  and the non-inverting input
and the non-inverting input  :
:
 |
(1) |
 is the differential-mode gain and
is the differential-mode gain and  is the common-mode
gain. It is desired that
is the common-mode
gain. It is desired that
 and
and
 ,
i.e., the output is only proportional to the difference
,
i.e., the output is only proportional to the difference  between
the two inputs. The common-mode rejection ratio (CMRR) is defined as the
ratio between differential-mode gain and common-mode gain:
between
the two inputs. The common-mode rejection ratio (CMRR) is defined as the
ratio between differential-mode gain and common-mode gain:
 |
(2) |
Also, as the output










As 









 , output impedance
, output impedance
 and voltage gain
and voltage gain  , as shown in (B). Then the voltage follower
can be modeled by its input impedance
, as shown in (B). Then the voltage follower
can be modeled by its input impedance  , output impedance
, output impedance  ,
and voltage gain
,
and voltage gain  , as shown in (C).
, as shown in (C).
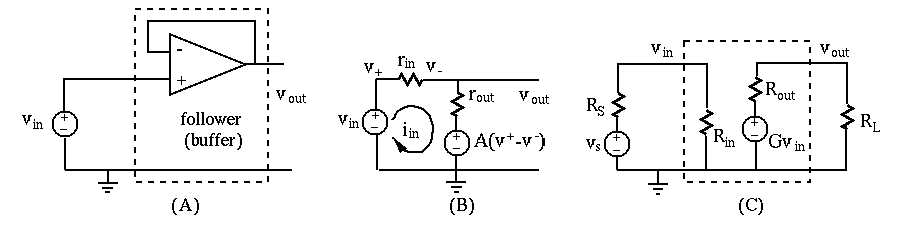
Specifically, 



 :
:
Applying KVL to the loop we get
 |
(3) |
 we get the input impedance:
we get the input impedance:
 |
(4) |
 :
:
The open-circuit output voltage is
 |
(5) |
 |
(6) |
 and
and  . We therefore have
. We therefore have
 |
(7) |
 :
:
With a short-circuit load 

 |
(8) |
 , we get the output impedance
(Thevenin's model):
, we get the output impedance
(Thevenin's model):
 |
(9) |

In summary, the voltage follower has a unit voltage gain,
but much increased input resistance






Example:
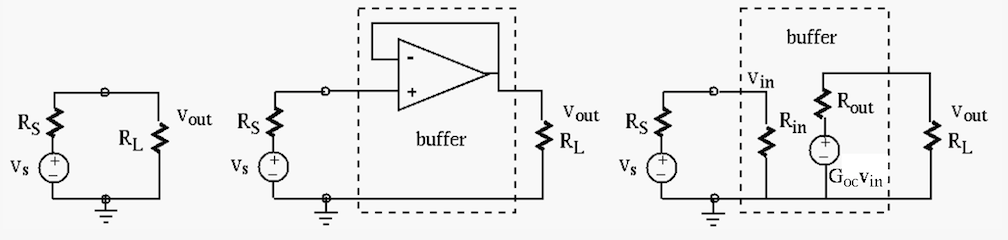
The figure on the left shows a circuit represented by a nonideal
voltage source, containing an ideal voltage source 



 |
(10) |
 due to the voltage drop
due to the voltage drop
 across the internal resistance
across the internal resistance  . For the
doutput voltage to be as close to the source as possible, the internal
resistance
. For the
doutput voltage to be as close to the source as possible, the internal
resistance  needs to be small compared to the load resistance
needs to be small compared to the load resistance  .
.
In the middle figure, a voltage follower (as a buffer) is inserted in
between the source and the load. The follower is modeled by its input
and output resistances 


 |
(11) |



 |
(12) |
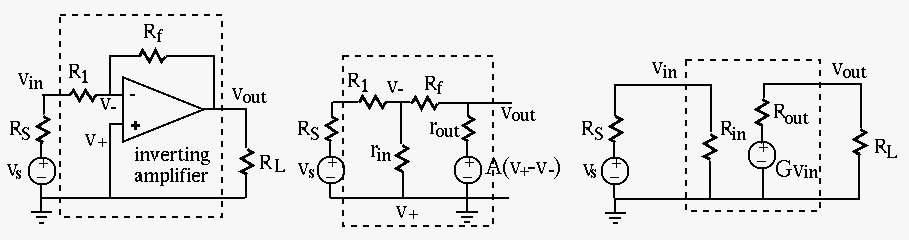
To simplify the analysis of the circuit based on the full model of the op-amp, we make certain approximations in the following.
 )
)
As





 |
(13) |
 we get
we get
 |
(14) |
![$\displaystyle v_{out}=v_{in}-(R_1+R_f) i_{in}
=v_{in}\left[1-\frac{(A+1)(R_1+R_f)}{(A+1)R_1+R_f}\right]
=v_{in}\frac{-AR_f}{(A+1)R_1+R_f}$](img77.svg) |
(15) |
 , we get the open-circuit voltage gain:
, we get the open-circuit voltage gain:
 |
(16) |
 .
.
This result can also be obtained under the virtual ground assumption


 i.e. i.e. |
(17) |
We find the input resistance 



 |
(18) |
 :
:
 |
(19) |
 |
 |
![$\displaystyle \frac{v_{in}-v^-}{R_1}
=\frac{v_{in}}{R_1}\left[1-\frac{R_f}{R_f+(A+1)R_1}\right]$](img86.svg) |
|
 |
 |
(20) |
 by
by  we get
Note that this input resistance is significantly smaller
than that of the voltage follower with
we get
Note that this input resistance is significantly smaller
than that of the voltage follower with
 !
!
 ):
):
 |
(22) |
 , the above becomes
, the above becomes
 |
(23) |
 we get
we get
 |
(24) |
 we get
we get
 |
(25) |
 |
 |
![$\displaystyle [v^--(-Av^-)]\frac{r_{out}}{R_f+r_{out}}-Av^-
=v^-\left[(1+A)\frac{r_{out}}{R_f+r_{out}}-A\right]$](img95.svg) |
|
 |
 |
(26) |
 |
 |
 |
|
 |
 |
(27) |
 and
and
 .
.
In summary,
 |
(28) |
 |
(29) |
 |
(30) |
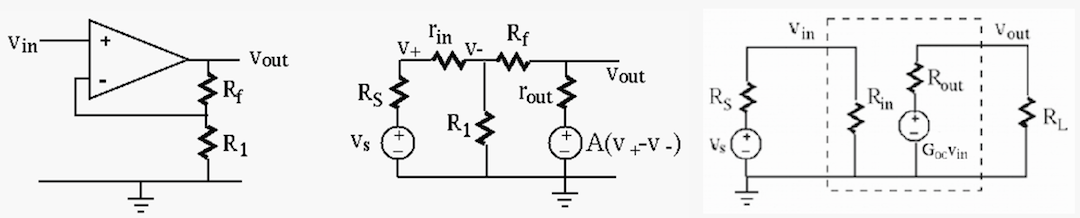
The three parameters of this non-inverting amplifier can be found to be (see here):
 |
(31) |
 |
(32) |
 |
(33) |
 , but smaller
, but smaller  and bigger
and bigger
 . In particular if
. In particular if  , this non-inverting amplifier
becomes a voltage follower with
, this non-inverting amplifier
becomes a voltage follower with  ,
,
 , and
, and
 .
.