Next: About this document ... Up: TwinT Previous: TwinT
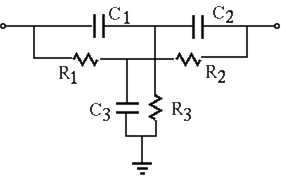
 (or
(or  ) network (see
here)
of three branches:
) network (see
here)
of three branches:
 (1)
(1)
 (2)
(2)
 and
and  is:
is:
 |
 |
 |
|
 |
 |
 . This is a first-order low-pass filter with cut-off
frequency at
. This is a first-order low-pass filter with cut-off
frequency at
 :
:
 (3)
(3)
 (or
(or  ) network of three branches:
) network of three branches:
 (4)
(4)
 (5)
(5)
 and
and  is:
is:
 |
 |
 |
|
 |
 |
 :
:
 (6)
(6)
As these two 




 (7)
(7)
 (8)
(8)
 -network (a voltage divider) is:
-network (a voltage divider) is:
 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
 |
Alternatively, we apply KCL at the middle points of the RCR and CRC
networks with 

 (9)
(9)
 and
and  , we get
, we get
 (10)
(10)
 (11)
(11)
 and
and  into this equation we get:
into this equation we get:
 (12)
(12)

 (13)
(13)
 .
.
Active twin-T filter
 (14)
(14)
 , i.e.,
, i.e.,
 .
.
 (15)
(15)
 and
and  , we get
, we get
 (16)
(16)
 , we get
, we get
 (17)
(17)
 |
 |
 |
|
 |
 |