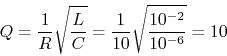- Use Matlab to plot the frequency response functions (FRF) of the
RC first-order low-pass (voltage across C is the output) and high-pass
(voltage across R is the output) filters. Assume
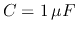 ,
,
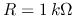 . Choose the range of frequency properly so that the
corner frequency is around the middle region of the plots.
. Choose the range of frequency properly so that the
corner frequency is around the middle region of the plots.
- Plot the linear gain and phase as a function of
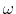 of
the two filters.
of
the two filters.
- Make the Bode plots (without using the built-in function Bode)
of both the gain (in log magnitude
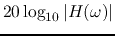 and
phase (between
and
phase (between 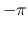 and
and 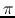 ) of the two filters (log scale in
frequency). The Matlab function semilogx can plot a function
) of the two filters (log scale in
frequency). The Matlab function semilogx can plot a function 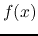 with log scale in
with log scale in 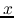 .
.
Solution: The first-order plots should be the same as those shown
in the lecture notes shown
here
with the only difference that the cornor (cut-off) frequency is at
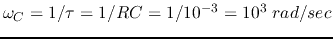 .
.
- Use Matlab to plot the frequency response functions (FRF) of the
RLC second-order low-pass (voltage across C as the output), band-pass
(voltage across R as the output), and high-pass (voltage across L as
the output) filters. Assume
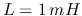 ,
, 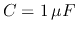 ,
, 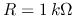 .
Choose the range of frequency properly so that the natural frequency
is around the middle region of the plots.
.
Choose the range of frequency properly so that the natural frequency
is around the middle region of the plots.
- Plot the linear gain and phase as a function of
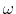 of the
three filters.
of the
three filters.
- Make the Bode plots (without using the built-in function Bode)
of both the gain and phase of the three filters (log scale in frequency).
Solution:
- In the circuit below,
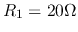 ,
, 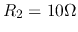 ,
, 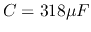 ,
and the sinusoidal voltage source is
,
and the sinusoidal voltage source is
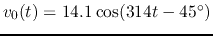 .
Find the complete voltage response
.
Find the complete voltage response 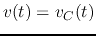 across
across 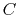 and
and 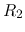 after
the switch closes at
after
the switch closes at 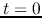 .
.
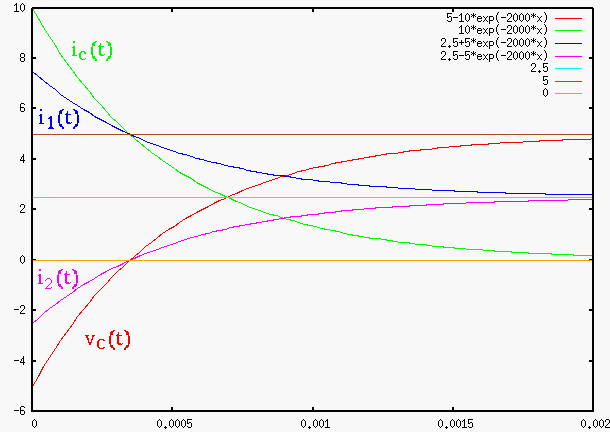
Solution:
- First find phasor representation of the voltage source:
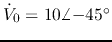 and the impedance of the capacitor:
and the impedance of the capacitor:
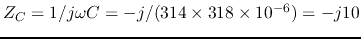 .
.
- Find
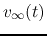 :
:
- Find
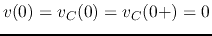
- Find
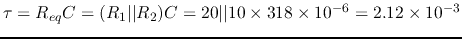
Now we get:
- The RCL series circuit can be used as a filter when the voltage across
all three components is the input and the voltage across any of the
three components is treated as output. Find the resonant frequency
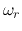 (at which the output is maximized) in terms of the natural
frequency
(at which the output is maximized) in terms of the natural
frequency
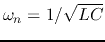 , when (1) voltage
, when (1) voltage 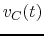 across C
is treated as output, and (2) voltage
across C
is treated as output, and (2) voltage 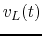 across L is treated as
output.
across L is treated as
output.
The frequency response functions 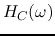 and
and 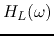 may have a peak, i.e.,
may have a peak, i.e.,
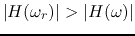 for any
for any
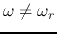 , when
, when 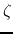 is small enough, but it may not have such a
peak if
is small enough, but it may not have such a
peak if 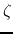 is too large. Find the critical value
is too large. Find the critical value 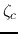 so
that for any
so
that for any 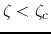
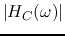 and
and 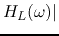 will
have a peak at
will
have a peak at
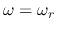 , but such a peak no longer exist when
, but such a peak no longer exist when
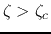 .
.
Solution: See
here
- An RCL series circuit composed of
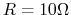 ,
, 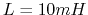 and
and
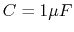 is connected to an input AC voltage
is connected to an input AC voltage
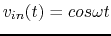 .
.
- Find the quality factor
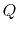 and resonant frequency
and resonant frequency 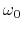 .
.
- Assume the voltage
 across
across 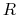 is taken as the output voltage.
Find the bandwidth of the circuit. Also, use any software (e.g., Matlab)
to plot the ratio of the magnitudes between the output and input voltages
is taken as the output voltage.
Find the bandwidth of the circuit. Also, use any software (e.g., Matlab)
to plot the ratio of the magnitudes between the output and input voltages
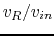 as a function of frequency
as a function of frequency 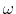 .
.
- Assume the voltage
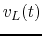 across
across 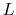 is taken as the output voltage.
plot the ratio
is taken as the output voltage.
plot the ratio 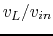 as a function of frequency
as a function of frequency 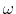 .
.
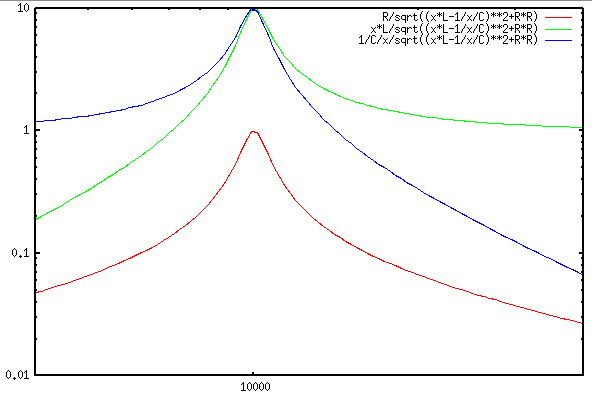
- Assume the voltage
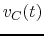 across
across 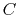 is taken as the output voltage.
plot the ratio
is taken as the output voltage.
plot the ratio 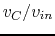 as a function of frequency
as a function of frequency 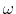 .
.
Solution:
- A series circuit composed of a capacitor and an inductor is to be
resonant at 800 kHz with voltage input. Specify the value of
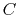 for the
capacitor required for the given inductor with
for the
capacitor required for the given inductor with 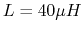 and an internal
resistance
and an internal
resistance
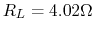 , and predict the bandwidth. Assume the capacitor
is ideal, i.e., it introduces no resistance.
, and predict the bandwidth. Assume the capacitor
is ideal, i.e., it introduces no resistance.
Solution:
As
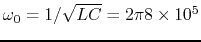 , and
, and
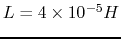 , we
can find
, we
can find 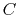 to be
to be
Next find the quality factor:
then the bandwidth is
- Design a series circuit to be resonant at 800 kHz with a bandwidth
of 32 kHz. The inductor has
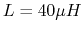 and
and
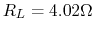 . Find the
capacitance
. Find the
capacitance 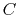 needed for the desired resonant frequency. In order to
satisfy the desired bandwidth, you may also need to include a resistor in
the circuit.
needed for the desired resonant frequency. In order to
satisfy the desired bandwidth, you may also need to include a resistor in
the circuit.
Solution: Based on the desired resonant frequency and bandwidth,
the quality factor needs to be
Since 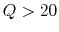 , the resonant frequency is approximately
, the resonant frequency is approximately
However, the quality factor of the parallel circuit is
twice the desired 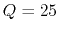 , we have to double the resistance
, we have to double the resistance 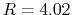 to
to
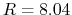 to reduce
to reduce 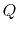 by half.
by half.
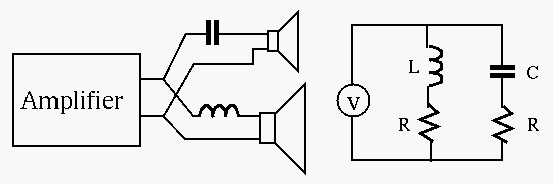
- The function of a loudspeaker crossover network is to channel
frequencies higher than a given crossover frequency
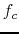 into the
high-frequency speaker (``tweeter'') and frequencies below
into the
high-frequency speaker (``tweeter'') and frequencies below 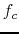 into
the low-frequency speaker (``woofer''). One such circuit is shown below.
Assume the resistances of the tweeter is
into
the low-frequency speaker (``woofer''). One such circuit is shown below.
Assume the resistances of the tweeter is 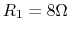 and that of the
woofer is
and that of the
woofer is 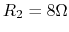 , the voltage amplifier can be modeled as an
ideal voltage source, and the crossover frequency is
, the voltage amplifier can be modeled as an
ideal voltage source, and the crossover frequency is 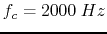 .
Design the network in terms of
.
Design the network in terms of 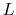 and
and 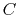 so that
so that 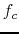 is the corner
freqnency or half-power point of each of the two speaker circuits. Give
the expression of the power
is the corner
freqnency or half-power point of each of the two speaker circuits. Give
the expression of the power 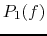 and
and 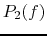 of the speakers as a
function of frequency
of the speakers as a
function of frequency 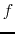 and crossover frequency
and crossover frequency 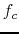 , and sketch them.
Assume the RMS of the input voltage is 1V.
, and sketch them.
Assume the RMS of the input voltage is 1V.
Solution
The RMS voltage across the tweeter is
If 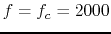 is at half-power point (
is at half-power point (
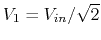 ), the real and
imaginary parts of the denominator should be equal and we get
), the real and
imaginary parts of the denominator should be equal and we get
The RMS voltage across the woofer is
If 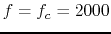 is at half-power point (
is at half-power point (
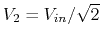 ), the real and
imaginary parts of the denominator should be equal and we get
), the real and
imaginary parts of the denominator should be equal and we get
The power plots:
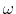 of
the two filters.
of
the two filters.
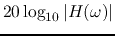 and
phase (between
and
phase (between 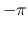 and
and 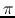 ) of the two filters (log scale in
frequency). The Matlab function semilogx can plot a function
) of the two filters (log scale in
frequency). The Matlab function semilogx can plot a function 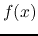 with log scale in
with log scale in 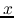 .
.
![]() .
.
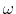 of the
three filters.
of the
three filters.


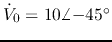 and the impedance of the capacitor:
and the impedance of the capacitor:
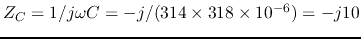 .
.
 :
:
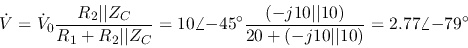
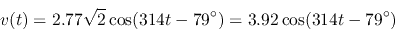
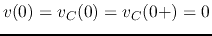
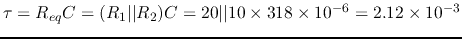
![]() and
and ![]() may have a peak, i.e.,
may have a peak, i.e.,
![]() for any
for any
![]() , when
, when ![]() is small enough, but it may not have such a
peak if
is small enough, but it may not have such a
peak if ![]() is too large. Find the critical value
is too large. Find the critical value ![]() so
that for any
so
that for any ![]()
![]() and
and ![]() will
have a peak at
will
have a peak at
![]() , but such a peak no longer exist when
, but such a peak no longer exist when
![]() .
.
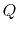 and resonant frequency
and resonant frequency 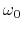 .
.
 across
across 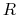 is taken as the output voltage.
Find the bandwidth of the circuit. Also, use any software (e.g., Matlab)
to plot the ratio of the magnitudes between the output and input voltages
is taken as the output voltage.
Find the bandwidth of the circuit. Also, use any software (e.g., Matlab)
to plot the ratio of the magnitudes between the output and input voltages
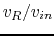 as a function of frequency
as a function of frequency 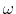 .
.
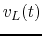 across
across 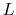 is taken as the output voltage.
plot the ratio
is taken as the output voltage.
plot the ratio 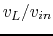 as a function of frequency
as a function of frequency 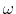 .
.
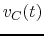 across
across 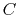 is taken as the output voltage.
plot the ratio
is taken as the output voltage.
plot the ratio 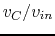 as a function of frequency
as a function of frequency 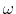 .
.

![]() , and
, and
![]() , we
can find
, we
can find ![]() to be
to be