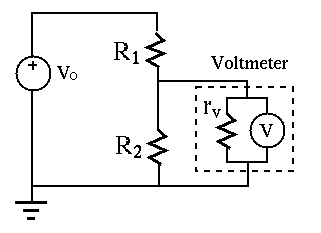
(b) A voltmeter can be modeled by an ideal meter with infinite impedance in parallel
with an internal (or input) impedance ![]() . To minimize the influnce of the voltmeter
on the circuit during the measurement, should
. To minimize the influnce of the voltmeter
on the circuit during the measurement, should ![]() be minimized or maximized?
be minimized or maximized?
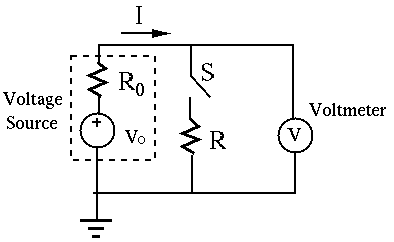
(c) Calculate current ![]() and voltage
and voltage ![]() in the simple circuit below, assuming
in the simple circuit below, assuming
![]() ,
, ![]() and the measuring meters are not connected, i.e., the ammeter
is short circuit, the voltmeter is open circuit.
and the measuring meters are not connected, i.e., the ammeter
is short circuit, the voltmeter is open circuit.
(d) What is the reading on the ammeter with ![]() inserted in the circuit
as shown? Assume the voltmeter is not connected.
inserted in the circuit
as shown? Assume the voltmeter is not connected.
(e) What is the reading on the voltmeter with
![]() , connected
to the circuit as shown? Assume the ammeter is not connected.
, connected
to the circuit as shown? Assume the ammeter is not connected.
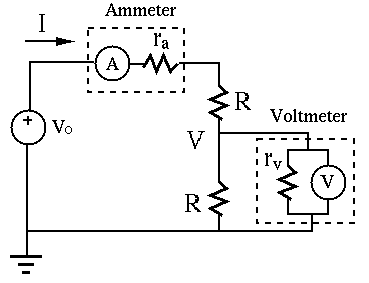
Solution:
(a) ![]() should be minimized, ideally, zero.
should be minimized, ideally, zero.
(b) ![]() should be maximized, ideally, infinity.
should be maximized, ideally, infinity.
(c)
(d)
(e)
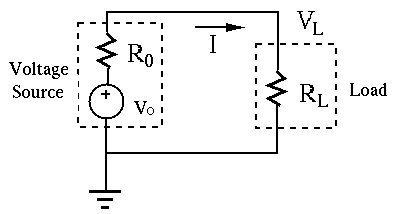
Solution:
(a) When
![]() ,
,
(b) ![]() .
.
(c) To maximize ![]() , we want maximize
, we want maximize ![]() and minimize
and minimize ![]() .
.
- When the battery is fresh, it is found
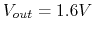 when the switch is open
and
when the switch is open
and 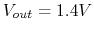 when the switch is closed. Find the internal impedance
when the switch is closed. Find the internal impedance 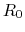 .
.
- The same battery is tested one year later, and
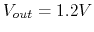 when the switch
is open and
when the switch
is open and 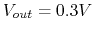 when the switch is closed. Find the internal impedance
when the switch is closed. Find the internal impedance
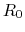 .
.
Solution:
Solution:
Solving this equation for