Solution:
(b) Replace one of the two bulbs by another bulb labeled as 110V 15W, and find the power consumption of each of the bulbs. What will happen to each of the two bulbs? (Note that when the power consumption by a bulb is larger than the specified wattage, it will be burned out!)
Solution:
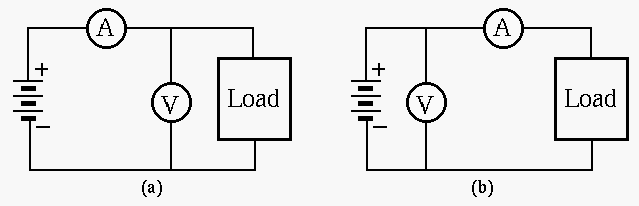
- What are required of the ammeter and the voltmeter to minimize their
influences on the measurements?
Solution: The ammeter should have minimum (ideally 0) impedance while the voltmeter should have maximum (ideally infinity) impedance.
- How would the ammeter and the voltmeter affect the measurement of the current and the voltage in either of the configurations (a and b)?
Solution: In (a) the voltmeter will by-pass some current so that the actual current through the load is smaller than the reading of the ammeter.
In (b) the ammeter will cause some voltage drop and the actual voltage across the load is lower than the reading of the voltmeter.
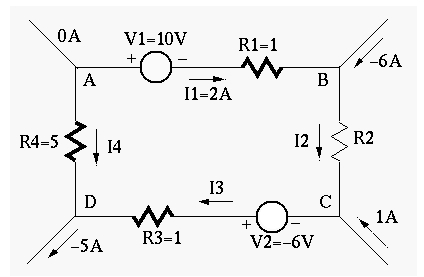
(Note: The direction of a current and the polarity of a voltage source can be assumed arbitrarily. To determined the actual direction and polarity, the sign of the values also should be considered. For example, a current labeled in left-to-right direction with a negative value is actually flowing right-to-left.)
Solution:
- apply KCL to node B:
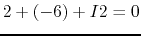 ,
, 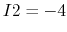
- apply KCL to node C:
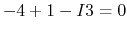 ,
, 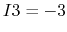
- apply KCL to node D:
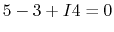 ,
, 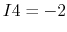
- apply KVL to loop ABCD:
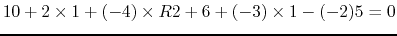 ,
,
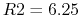
- apply KVL to loop BDA:
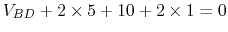 ,
,
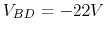 , or
, or
- apply KVL to loop BDC:
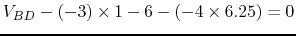 ,
,
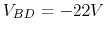
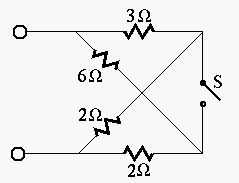
Solution:
before S is closed,
![]()
after S is closed,
![]()
(Hint: apply a test voltage ![]() across the terminals and the
equivalent resistance can be found to be
across the terminals and the
equivalent resistance can be found to be
![]() .
The circuit can be solved by applying KCL to
.
The circuit can be solved by applying KCL to ![]() and
and ![]() .)
.)
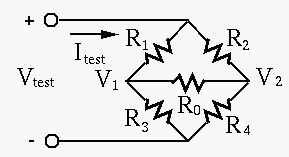
Solution:
solving these we get
solving to get
Note that in this case
Alternatively, based on delta-Y conversion (to be considered later), the
triangle (delta) formed by ![]() ,
, ![]() , and
, and ![]() can be coonverted to a Y
configuration with
can be coonverted to a Y
configuration with ![]() (top),
(top), ![]() (left), and
(left), and ![]() . Then
we have
. Then
we have ![]() and
and ![]() . Their parallel combination is
. Their parallel combination is
![]() , in series with
, in series with ![]() , i.e., the total resistance
is
, i.e., the total resistance
is
![]() . However, this approach does not reveal the fact that
. However, this approach does not reveal the fact that
![]() can take any value without changing
can take any value without changing ![]() .
.
- DC Voltage measurement: DC voltages in these ranges can be measured
0-2.5, 0-10, 0-50, and 0-250 (all in volts). Use a 4-position rotary switch
to select one of the four ranges as shown in the figure below. For example,
when the range of 0-10 is selected, the needle display will reach full scale
when the voltage being measured is 10 V. The circuit is shown below. Determine
all resistances labeled.
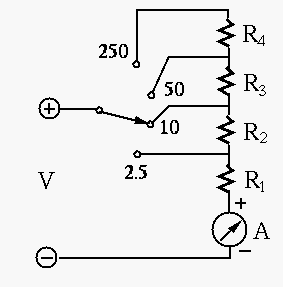
Solution:
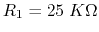 ,
,
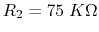 ,
,
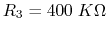
and
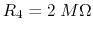 .
.
- AC Voltage measurement: To measure an AC voltage (in terms of its
RMS value), it first needs to be converted into a DC voltage. This can
be achieved by a diode which only allows the current to pass in one
direction (along the arrow) but not the other. This process is called
rectification. The diode will also cause a voltage drop of 0.7 volt
along the direction. The actual reading of the meter reflects the
average value of the rectified current. Find the resistance
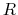 so
that when the incoming AC voltage is
so
that when the incoming AC voltage is 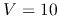 volt (RMS), the meter shows
a full scale display.
volt (RMS), the meter shows
a full scale display.
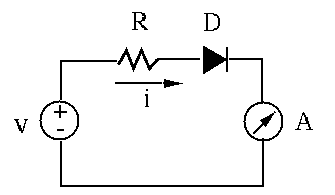
Solution: The peak value of voltage is
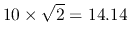 ,
which is reduced (due to voltage drop of the diode) to
,
which is reduced (due to voltage drop of the diode) to
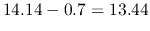 .
The average value of the rectified voltage is
.
The average value of the rectified voltage is
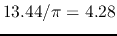 . For the
meter to have a full scale display, the current need to be
. For the
meter to have a full scale display, the current need to be
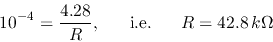
The internal resistance of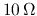 can be neglected.
can be neglected.
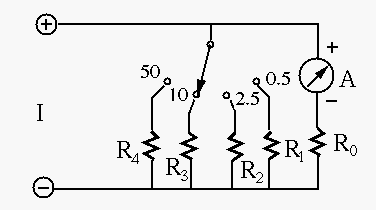
- DC current measurement: measure currents in these ranges (all in mA):
0-0.5, 0-2.5, 0-10, 0-50. Use a 4-position rotary switch to select one
of the four ranges as shown in the figure below. For example, when the
range of 0-10 is selected, the needle display will reach full scale when
a 10 mA current is measured. Determine all resistances labeled. Use
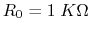 .
.
Solution: Voltage across input is
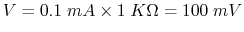 .
Therefore
.
Therefore
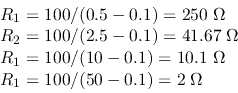
- Resistance measurement: The circuit for resistance measurement is
provided as shown below, where
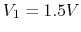 . Determine the values for the
resistors labeled as
. Determine the values for the
resistors labeled as 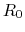 ,
, 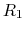 ,
, 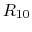 ,
, 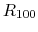 and
and 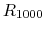 and
and 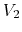 so that the needle display of the meter is full scale
(
so that the needle display of the meter is full scale
(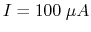 ) when the resistor
) when the resistor 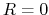 being measured (between the
two leads labeled + and -) is zero, or half scale (
being measured (between the
two leads labeled + and -) is zero, or half scale (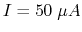 ) when
the value of
) when
the value of 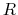 and the position of he two synchronized rotary switches
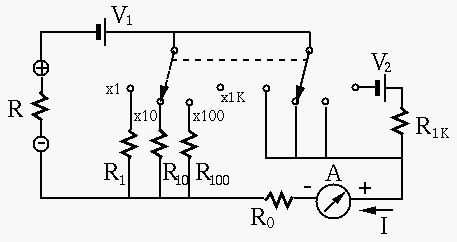
are given in each of the four case shown in the table:
and the position of he two synchronized rotary switches
are given in each of the four case shown in the table:
positions 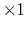
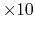
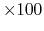
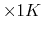
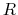 values
values20 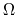
200 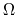
2000 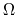
20 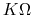
Solution:
- First determine
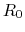 : when
: when 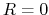 , we get
, we get
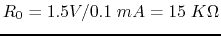 .
.
- When
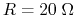 , the current through meter
, the current through meter 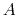 should be:
should be:
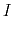
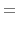
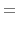
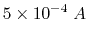
Given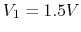 ,
, 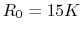 and
and 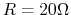 , we can solve this
equation to get
, we can solve this
equation to get
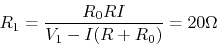
- When
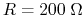 , solving the above equation we get
, solving the above equation we get
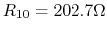 .
.
- When
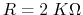 , solving the above equation we get
, solving the above equation we get
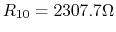 .
.
- When
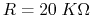 , we need to determine
, we need to determine 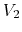 and
and
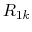 so that
so that
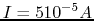 , and also when
, and also when 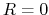 ,
,
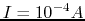 .
. 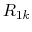 and
and 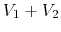 can be found by solving
these equations:
can be found by solving
these equations:
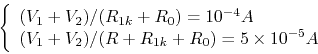
Solving we get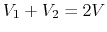 ,
,
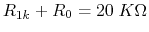 , i.e.,
, i.e.,
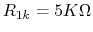 ,
, 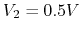
- First determine