


Next: About this document ...
Up: averagevalue
Previous: Average Value of Sinusoids
The effective value of a time-varying current 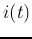 or voltage is the
constant value of current
or voltage is the
constant value of current 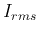 or voltage
or voltage 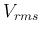 that in period
that in period
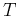 would transfer the same amount of energy:
would transfer the same amount of energy:
i.e.,
As 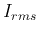 or
or 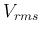 is the ``square root of the mean of the squared value'',
it is also called the root-mean-square (rms) current or voltage.
is the ``square root of the mean of the squared value'',
it is also called the root-mean-square (rms) current or voltage.
For a sinusoidal variable
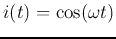 , we have
, we have
(Recall trigonometric identity:
![$\cos^2\alpha=[1+\cos(2\alpha)]/2$](img21.png) .)
Similarly, we also have
.)
Similarly, we also have
Ruye Wang
2016-01-17
![]() or voltage is the
constant value of current
or voltage is the
constant value of current ![]() or voltage
or voltage ![]() that in period
that in period
![]() would transfer the same amount of energy:
would transfer the same amount of energy:
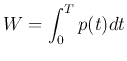
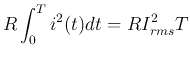
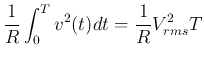
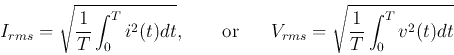
![]() , we have
, we have