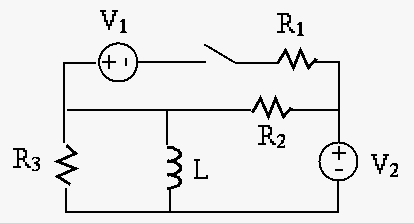
Next: About this document ... Up: midterm2_21f Previous: Instructions
 can be
approximated to be zero.
can be
approximated to be zero.
 at which the
impedance of the model is maximized.
at which the
impedance of the model is maximized.
 at which the
impedance of the model is minimized.
at which the
impedance of the model is minimized.
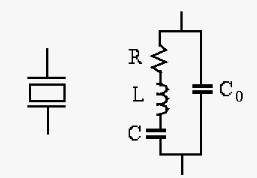
 ,
,  and
and  between the source
between the source  and the load
and the load  is to pass the
fundamental frequency
is to pass the
fundamental frequency  without attenuation but completely
block the 2nd harmonic
without attenuation but completely
block the 2nd harmonic
 . Given
. Given  , find
, find  and
and  .
.
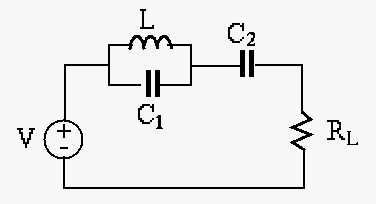
 ,
,  ,
,  ,
,
 ,
,  ,
,  . The circuit is in steady state when
. The circuit is in steady state when
 . Find current
. Find current  through
through  when switch is closed at
when switch is closed at
 .
.