Find the two currents labeled as ![]() and
and ![]() in the figure.
in the figure.
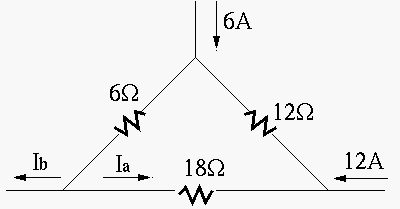
Solution:
By KCL (observation), ![]() .
.
Use loop current method to around the loop and get:
Solving this we get
Use branch current method. Assume currents going through 1![]() , 2
, 2![]() and 3
and 3![]() resistors are, respectively,
resistors are, respectively, ![]() ,
, ![]() and
and ![]() . Using KCL
and KVL, we get
. Using KCL
and KVL, we get
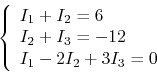
Solving this we get:
Alternatively, one can use superposition theorem. First, turn the 6A current
off and get
Second, turn the 12A off and get
Now we have
Find the voltage ![]() across the 2
across the 2![]() resistor (with assumed polarity shown),
and the current
resistor (with assumed polarity shown),
and the current ![]() through the 1
through the 1![]() voltage source (with assumed direction shown).
voltage source (with assumed direction shown).
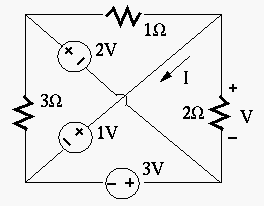
Solution:
Assume lower-left node is grounded as 0V. upper-left node is 5V, upper-right
node is 1V, and lower-right node is 3V. Voltage across ![]() resistor is
resistor is
![]() . Current through
. Current through ![]() resistor (right-ward) is 4A, current
through
resistor (right-ward) is 4A, current
through ![]() resistor (up-ward) is 1A, Applying KCL to upper-rigt node,
we get
resistor (up-ward) is 1A, Applying KCL to upper-rigt node,
we get ![]() .
.
Or, use superposition theorem:
- short the 1V and 2V sources,
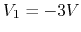 ,
,
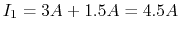
- short the 1V and 3V sources,
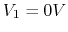 ,
, 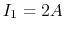
- short the 2V and 3V sources,
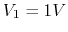 ,
,
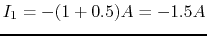
The following two parts of the problem are independent, each worth 20 pts.
- Find the resistance
 so that the voltage across the resistor is 1V.
so that the voltage across the resistor is 1V.
- Find the resistance
 so that the current through the resistor is 0.2A.
so that the current through the resistor is 0.2A.
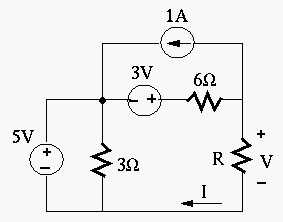
Solution:
The problems can be most easily solved by assuming the desired voltage/current
and then figuring out the resistance ![]() needed.
needed.
Fiirst, if ![]() as desired, then the current (rightward) through the
as desired, then the current (rightward) through the ![]() resistor is
resistor is
![]() , and the current through
, and the current through ![]() (downward) is
(downward) is
![]() , and we get
, and we get ![]() .
.
Second, if ![]() as desired, then the current (rightward) through
as desired, then the current (rightward) through ![]() resistor has to be
resistor has to be ![]() and the voltage drop across it is
and the voltage drop across it is ![]() (positive on
the left). Now the voltage to the right of the
(positive on
the left). Now the voltage to the right of the ![]() resistor is
resistor is
![]() ,
and
,
and
![]() .
.
Superposition method could also be used.
- Only turn 3V voltage source on (5V shorted together with
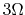 resistor, 1A
current source is open), we get
resistor, 1A
current source is open), we get
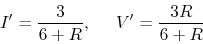
- Only turn 5V voltage source on (3V shorted, 1A current source is open), we get
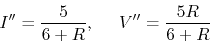
- Only turn 1A current source on (3V and 5V are both shorted), we get
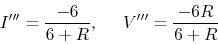
Solving these for
Alternatively, we can use Thevenin's theorem or Norton's theorem by treating the
![]() as a load. In either case, we need to find the internal resistance of the rest
of the circuit excluding R. When all energy sources are turned off, the internal
resistance is simply
as a load. In either case, we need to find the internal resistance of the rest
of the circuit excluding R. When all energy sources are turned off, the internal
resistance is simply ![]() .
.
- Find open circuit voltage
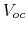 :
:
Use superposition, when current source is open,
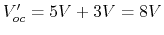 ; when
voltage sources are short,
; when
voltage sources are short,
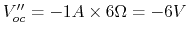 . Therefore
. Therefore
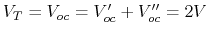
- Find short circuit current
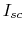 :
:
Use superposition, when current source is open,
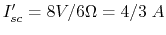 ;
when voltage sources are short,
;
when voltage sources are short, 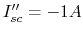 . Therefore
. Therefore
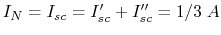 , which is consistent with the previous
result:
, which is consistent with the previous
result:
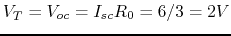 .
.