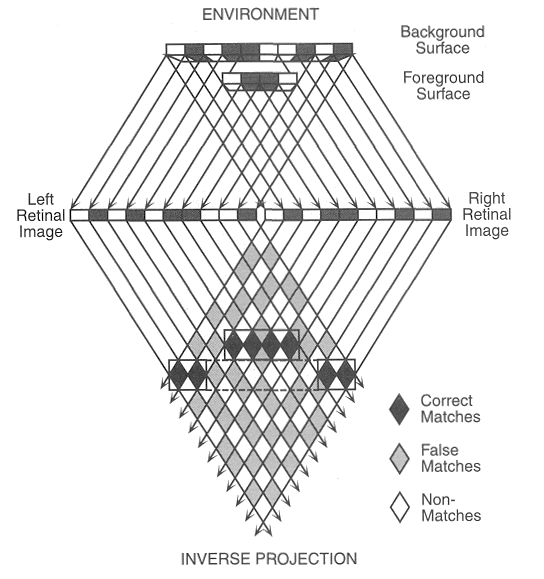
- Surface Opacity The object surface is opaque so that along a ray only the point closest to the eye is visible;
- Surface Continuity The surface is in general continuous and smooth, i.e., neighboring points tend to have same or similar depths.
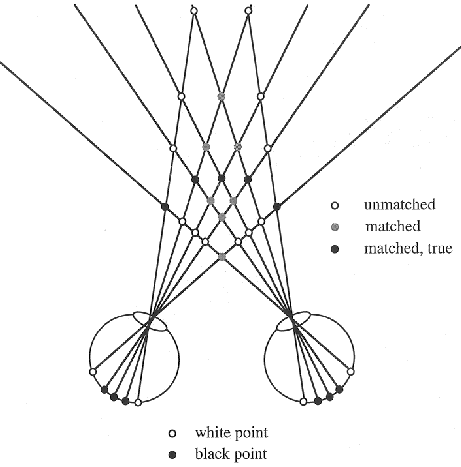
Marr and Poggio (1977) proposed an algorithm to solve correspondence problem based on the gray levels (assumed to be black and white for simplicity) of the two retina images. Their algorithm has the following two phases:


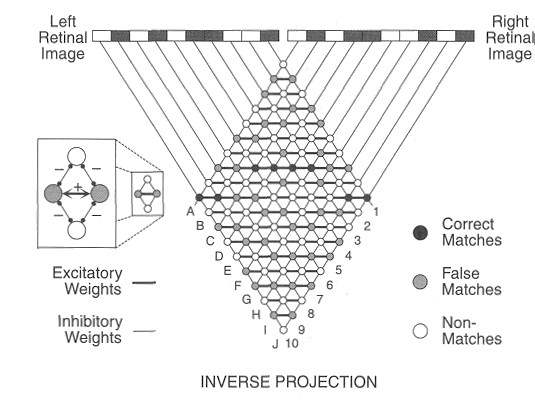
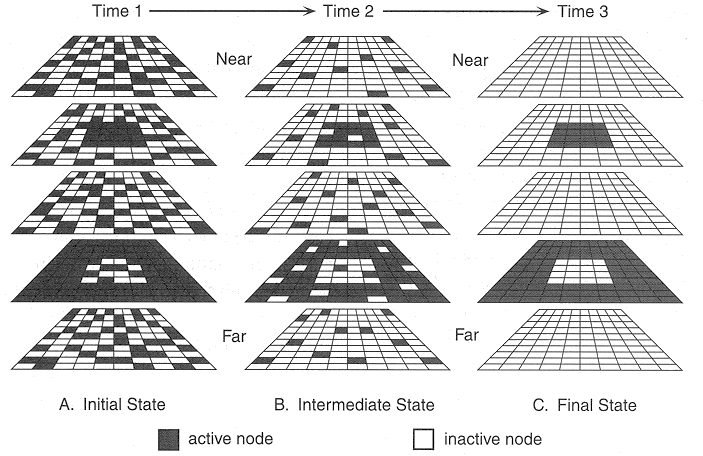
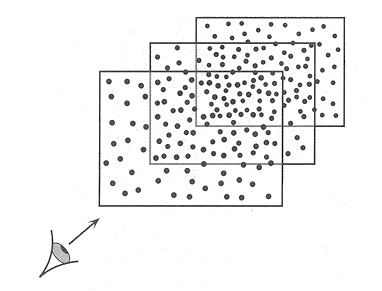
While this algorithm successfully solve the correspondence problem, it is seriously challenged by the random-dot experiment (Prazdny 1984) as shown below, where neighboring points in the retina images may be from 3D points of different depths, i.e., the assumption of surface continuity is no longer valid. However, human subjects can solve this stereogram effortlessly.
Another algorithm by Jones and Malik (1992) is based on the idea of spatial filtering. This method assumes a set of biologically inspired spatial filters for different spatial frequencies (scales) and different orientations is available at every retina location. Each local region in the retina image is filtered by this set of filters and the corresponding outputs are stored as the elements of a vector representing the region. Instead of matching the pixels in the left and right retina images, this method matches a vector for a position in the first image to the vectors of a set of regions in the neighborhood (with different lateral displacements) of the corresponding position in the other image. The bionocular disparity is obtained from the two vectors that match the best.