


Next: Induced Color
Up: No Title
Previous: Linear Models of Reflectance
When both the illumination and the reflectance are linearly modeled
we get a bilinear model which can be used to address the color constancy issue
by describing the responses of the p (p=3 for human eye) types of sensors
as
where the ckji's are a set of p by m by n coefficients representing the
response of the ith cones to the jth basis function for reflectance illuminated
by the ith basis function for the illumination, which can be determined given
the kth basis functions
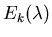 for the illumination, the jth basis
functions
for the illumination, the jth basis
functions
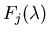 for reflectance, and
for reflectance, and
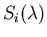 ,
the sensitivity
of the ith sensors:
,
the sensitivity
of the ith sensors:
The purpose here is to use the known responses of the p sensors ri's,
as well as our knowledge, the known bilinear coefficients cjki's, to
determine the unknown weights (descriptors) fj's for the reflectance and
ek's for the illumination so that they can be determined independently. In
general unique determination of mn variables requires the same number of
equations, i.e., p=mn sensors are needed. While p<mn, additional conditions
must be imposed in order to make the problem solvable, such as
- The average of all surfaces in the image is gray;
- The brightest surface in the image is a uniform reflector;
- Specularities or glossy surfaces are available in the image;
- The surfaces are observed multiple times under different illuminations.
Many methods along this line have been proposed in the recent years.
To find how the sensors respond to the same surface with different
illuminations and how the responses under different illuminations are related,
we apply the linear model for reflectance and write the responses as
where
which can be obtained given the specific illumination
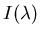 ,
the
cone sensitivities
,
the
cone sensitivities
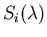 and the basis functions for the reflectance
and the basis functions for the reflectance
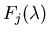 .
If we use only n=3 terms to approximate any reflectance,
the cij's can be written as a 3 by 3 matrix
.
If we use only n=3 terms to approximate any reflectance,
the cij's can be written as a 3 by 3 matrix
and three equations above can be written in vector form as
r = C f
The responses to the same surface but under a different illumination can also
be written
r'= C' f
Now the two sets of cone responses are related by
r=CC'-1 r'
i.e., the cone responses under one illumination is linearly related to the
responses under a different illumination.
For the blue-sky illumination, we have
For the tungsten bulb,
Now the responses to an arbitrary surface illuminated by the tungsten
bulb are linearly related to the responses to the same surface illuminated by
the blue sky by



Next: Induced Color
Up: No Title
Previous: Linear Models of Reflectance
Ruye Wang
2000-04-25
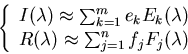
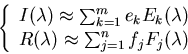
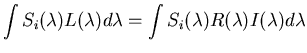
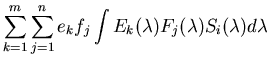
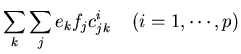
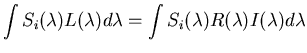
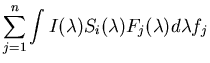
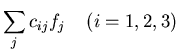
![\begin{displaymath}C=\left[ \begin{array}{lll} c_{11} & c_{12} & c{13} \\
c_{21} & c_{22} & c{23} \\ c_{31} & c_{32} & c{33} \end{array} \right] \end{displaymath}](img65.gif)
![\begin{displaymath}C=\left[ \begin{array}{lll} 591.5 & 223.1 & -643.1 \\
477.6 & 376.9 & -564.5 \\ 267.6 & 487.5 & 350.4 \end{array} \right] \end{displaymath}](img66.gif)
![\begin{displaymath}C=\left[ \begin{array}{lll} 593.5 & 68.4 & -646.7 \\
445.8 & 312.8 & -564.3 \\ 152.5 & 278.5 & 185.5 \end{array} \right] \end{displaymath}](img67.gif)
![\begin{displaymath}r=\left[ \begin{array}{lll} 0.812 & 0.227 & 0.065 \\
-0.080 & 1.134 & 0.128 \\ 0.043 & -0.076 & 1.809 \end{array} \right] r'
\end{displaymath}](img68.gif)