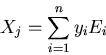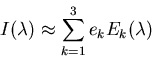Next: Nature May Have Its
Up: No Title
Previous: Homomorphic Filtering Algorithm
Given the light received by the eye
it is in general impossible to recover reflectance
 without knowing
the illumination
without knowing
the illumination
 .
However, under certain conditions, it is
possible to approximate both the reflectance and the illumination by some
linear combination of a finite number of basis functions:
.
However, under certain conditions, it is
possible to approximate both the reflectance and the illumination by some
linear combination of a finite number of basis functions:
and
so that the error under some definition (e.g., squared-error) is minimized.
For example, if squared error is used, we want
With these linear methods the task of recovering
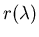 from
from
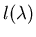 may become possible.
may become possible.
One example (Judd, Macadam, Wyszecki, 1964) is to approximate the power
spectral distributions of daylight under various conditions. A large number
(N=600) of daylight spectral distribution samples are collected at different
times of day, under different weather conditions and on different continents.
The visible wavelength band (400 to 700 nm) is sampled at 10 nm interval so
that each distribution is represented by n=31 numbers
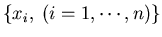 .
And the distributions are normalized so that they
are all equal to 100 at about the middle of the visible wavelength range
.
And the distributions are normalized so that they
are all equal to 100 at about the middle of the visible wavelength range
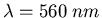 .
These N sample distributions can be considered as
N=600 vectors of n=31 dimensions
.
These N sample distributions can be considered as
N=600 vectors of n=31 dimensions
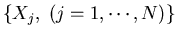 ,
where
,
where
![$X_j=[x_{1j},\cdots,x_{nj}]^T$](img38.gif) .
Three of them are shown in the figure.
.
Three of them are shown in the figure.
Then the principal component transform (PCT) is carried out to find a set
of bases so that the various daylight distributions can be approximated by a
linear combination of a small number of bases. Specifically, the PCT is carried
out in the following steps:
- Estimate the mean vector MX of Xj's
- Estimate the covariance matrix
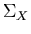 of Xj's
of Xj's
- Find eigenvalues
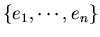 and eigenvectors
and eigenvectors
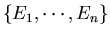 of the symmetric covariance matrix
of the symmetric covariance matrix 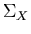 so that
so that
Here the eigenvalues are in descending order (from the largest to smallest) and
the corresponding eigenvectors are arranged accordingly (from the eigenvector
corresponding to the largest eigenvalue to that corresponding to the smallest).
The n eigenvectors
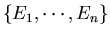 so obtained are the bases so that
each distribution Xj can be represented as the linear combination of them
so obtained are the bases so that
each distribution Xj can be represented as the linear combination of them
where the coefficient yi is the inner product of vectors Xj and Ei:
yi=EiT Xj
To use only a small number of the bases to approximate each distribution Xj,
we truncate the above summation to keep only the first m<n terms (the
principal components). It can be shown that the squared-error introduced
by this truncation is equal to the sum of the eigenvalues corresponding to the
those terms truncated. As the terms in the summation are arranged according to
the descending order of the eigenvalues, we know the error is minimum. In fact,
we can use as few as only m=3 terms to approximate all daylight distributions
with insignificant errors.
As shown in the figure, the first basis function happens to be the average of
all daylight distributions, and the other two basis functions represent
the short and long wavelength regions respectively.



Next: Nature May Have Its
Up: No Title
Previous: Homomorphic Filtering Algorithm
Ruye Wang
2000-04-25
![]() .
And the distributions are normalized so that they
are all equal to 100 at about the middle of the visible wavelength range
.
And the distributions are normalized so that they
are all equal to 100 at about the middle of the visible wavelength range
![]() .
These N sample distributions can be considered as
N=600 vectors of n=31 dimensions
.
These N sample distributions can be considered as
N=600 vectors of n=31 dimensions
![]() ,
where
,
where
![]() .
Three of them are shown in the figure.
.
Three of them are shown in the figure.
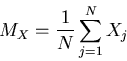
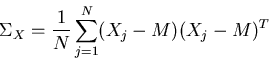
![]() so obtained are the bases so that
each distribution Xj can be represented as the linear combination of them
so obtained are the bases so that
each distribution Xj can be represented as the linear combination of them