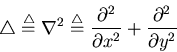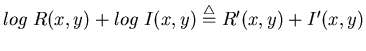Horn's Algorithm

A different computational model was proposed by Horn to account for the color constancy. This model is based on the same assumption that in general the illumination is a low spatial frequency signal while the reflectance is a high spatial frequency signal. To separate the high frequency components from the signal, a differential operation, can be considered. Since we want to treat edges of different orientations equally, the first order partial derivatives with respect to the two spatial directions x and y are not the best candidate as they are not rotationally symmetric. Therefore the second order spatial derivative, the Laplacian operator, is used:

$$\triangle \stackrel{\triangle}{=} \nabla^2 \stackrel{\triangl... ...frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}$$

• Take logarithm of the input light signal so that reflectance and illumination become additive:
  

  $$\stackrel{\triangle}{=} log\; L(x,y)=log \; [R(x,y) I(x,y)]$$ L'(x,y)

  $$log\; R(x,y)+log\; I(x,y)\stackrel{\triangle}{=}R'(x,y)+I'(x,y)$$ =

  
  

• Apply Laplacian operator to L'(x,y)=R'(x,y)+I'(x,y)
  
  $$d(x,y)=\triangle[R'(x,y)+I'(x,y)]=\triangle R'(x,y)+\triangle I'(x,y)$$
  
  

• Threshold
  
  $$t(x,y)=T[\triangle R'(x,y)+\triangle I'(x,y)]=\triangle R'(x,y)$$
  
  
  As we assume the illumination as a spatial function is much more homogeneous than the reflectance, the Laplas of the illumination 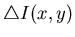$\triangle I(x,y)$ is small and therefore does not pass the threshold T.

• Take inverse Laplacian operation
  
  $$\triangle R'(x,y)=t(x,y)$$
  
  
  where R'(x,y) is the desired reflectance that can be obtained by solving this Poisson's equation using convolution
  
  $$R'(x,y)=\int \int _{-\infty}^{\infty} t(u,v)g(x-u,y-v) du\; dv$$
  
  
  where
  
  $$g(x,y)=\log(x^2+y^2)$$
  
  

• Take exponential operation
  
  R(x,y)=exp[ R'(x,y) ]