


Next: Photoreceptors and Perception of
Up: Color Matching and Trichromatic
Previous: Negative Tristimulus Values
Based on the observations of many color matching experiments, Grassman (1854)
summarized a set of eight axioms:
- Any color can be matched by a mixture of no more than three colors.
- A color match at one radiance level holds over a wide range of levels.
- Components of a mixture of colored lights cannot be resolved by the
human eye.
- The luminance of a color mixture is equal to the sum of the luminance of
its components.
- Law of addition -- if color M matches color N and color P matches color
Q, then color M mixed with color P matches color N mixed with color Q:
- Law of subtraction -- if the mixture of M and P matches the mixture
of N and Q, and if P matches Q, then M matches N:
- Transitive law -- if M matches N and N matches P, then M matches P:
- Color matching -- a given color
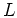 can be matched in one of three ways:
can be matched in one of three ways:
-
-
-
The 8th axiom is a summary of the color matching experiments discussed
previously. Because the principle of superposition holds in color mixing,
we can re-write a color match
as
Again, the symbol 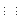 represents that the energy spectral distributions
on both sides are perceived as the same by the human eye, but as functions of
wavelength
represents that the energy spectral distributions
on both sides are perceived as the same by the human eye, but as functions of
wavelength 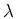 , they are not identical in general.
, they are not identical in general.



Next: Photoreceptors and Perception of
Up: Color Matching and Trichromatic
Previous: Negative Tristimulus Values
Ruye Wang
2013-09-25
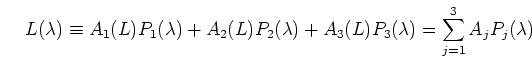
![]() represents that the energy spectral distributions
on both sides are perceived as the same by the human eye, but as functions of
wavelength
represents that the energy spectral distributions
on both sides are perceived as the same by the human eye, but as functions of
wavelength ![]() , they are not identical in general.
, they are not identical in general.