LMS Coordinate System

The response intensities of the L, M and S cones can be used as the bases of the 3D color space. Any perceived color is represented by a ray or a vector initiated from the origin along a certain direction determined by the proportions between the LMS responses. Note that every point in this 3D space represents a unique perceived color, but not a unique physical color of unique energy spectral distributions. In other words, a point in the color space represents all energy spectral distributions that are perceived the same.

All spectral (monochromatic) color of single wavelength ranging from 350 nm to 780 nm form a curved surface like a bent fan starting from the long wavelength at 780 nm very close to the L axis and ending at short wavelength at 350 very close to the S axis. This surface is everywhere convex. If this surface is truncated by a specific intensity the resulting edge is the spectrum locus. The line connecting the two end points (for red and violet) is called the purple line.

Since any color as a function of the wavelength $\lambda$ is a linear combination of all the spectral colors,

$$L(\lambda)=\int c(\lambda') \delta(\lambda-\lambda') d\lambda'$$

it is represented in the color space as a vector sum of the vectors along the spectral surface. We conclude that all perceivable colors are inside the conical solid enclosed by the spectral surface and the plane formed by the purple line and the origin. The cross section of this solid and the plane representing some certain intensity is called the chromaticity diagram representing all visible colors of the particular intensity. Usually this cross section in 3D color space is projected onto a 2D subspace spanned by two basis functions defined in some specific way (e.g., red and green).

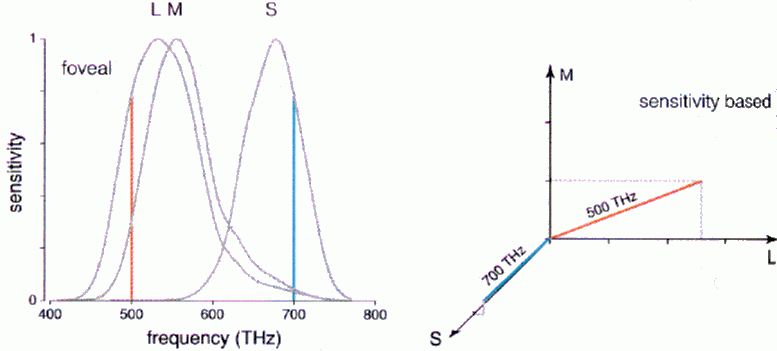
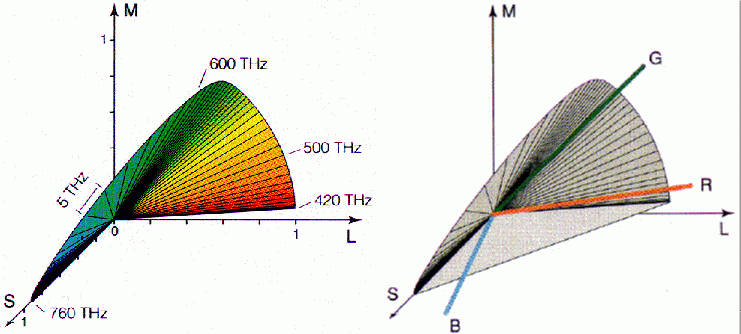
Note that energy distribution of light can be described by either wavelength $\lembda$ or frequency $f$ which are related by:

$$\lambda=c/f$$

where $c=3 \times 10^8 m/sec.$ is the speed of light. For example, wavelength $\lambda=500 nm$ is equivalent to

$$f=c/\lambda = 3 \times 10^8/500 \times 10^{-9}=600 \times 10^{-12}$$

hertz or $600$ Tera Hertz or THz.