Sensitivity functions

To explain the trichromatic theory, Thomas Young (1802) first postulated that at each point in the retina there must exist at least three tiny structures that are sensitive to red, green and violet. This theory was adopted and championed by Hermam von Helmholtz and came to be known as the Young-Helmholtz theory.

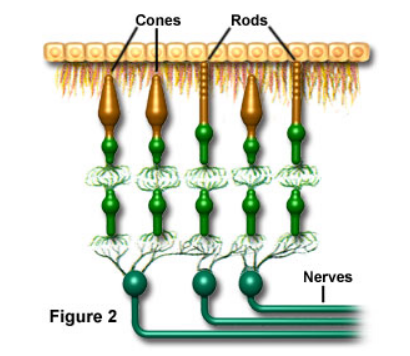
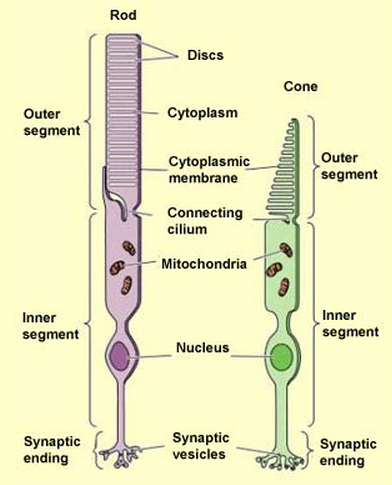
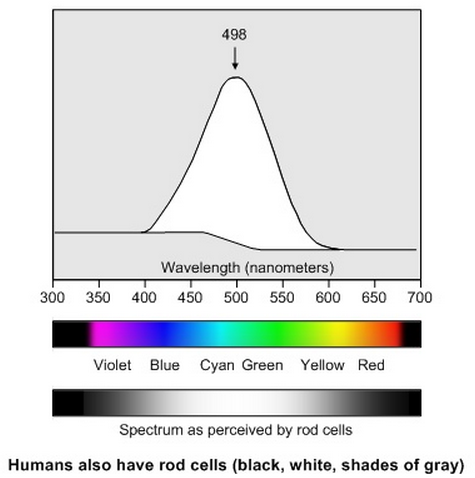
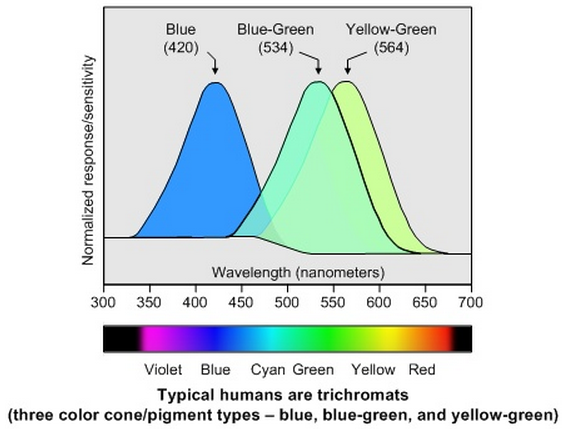
This theory was confirmed later by modern physiology. In the visual system of the primates, there are two types of photoreceptor cells called rods and cones. Rods are very sensitive to light and can respond to just a few photons. But the cones need significantly brighter light. There are three types of cone cells (called the S type, M type, and L type) with different sensitivities, responding to short, medium, and long wavelengths. Color vision is the result of these three types of cone cells. See here for more detailed discussions about these photoreceptor cells.

The physical intensity measurements of the electromagnetic energy distribution is related to the perceptual brightness and color by the scotopic (dim light mediated by the rods) and the photopic (bright light mediated by the cones) sensitivity or luminosity functions $S(\lambda)$. Specifically, the magnitude of the response of a photoreceptor (the firing rate) is determined by how much light is, or more specifically, how many photons are, absorbed by the photopigment of the photoreceptors. The more light a receptor catches, the stronger its response will be, and the more sensitive the receptor becomes. This property of the photoreceptors can be represented by its photon capture rate (number of photons absorbed per unit time), or its sensitivity, denoted by $S(\lambda)$ as a function of wavelength $\lambda$. 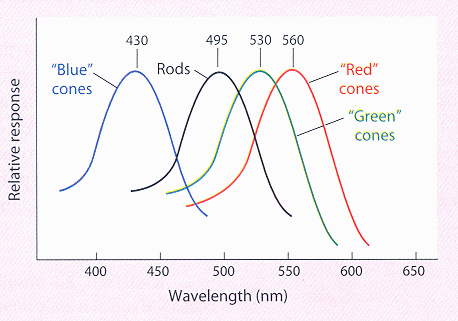The sensitivity functions of the three types of cone cells can be denoted by $S_i(\lambda)\;\;\;(i=1,2,3)$ which peak approximately at 560 nm, 530 nm and 430 nm respectively, as shown.

If the light received by the retina is $L(\lambda)$, then the response of a photoreceptor is proportional to the total number of photons absorbed, which can be obtained by

$$r=\int S(\lambda) L(\lambda) d\lambda$$