Applications

The Haar transform is a wavelet transform. For example, when $N=8$, the transform matrix is

$$H_8=\frac{1}{\sqrt{8}}\left[ \begin{array}{cccccccc} 1 & 1 & ... ...\\ \psi_{2,1}(t) \psi_{2,2}(t) \psi_{2,3}(t) \end{array}$$

The idea of Laplacian pyramid discussed before is very similar to wavelet transform. The forward transform is the Gaussian (low-pass) filtering and down-sampling process to obtain the Gaussian pyramid (the scaling coefficients) composed of images $f_1, f_2, \cdots$, and the Laplacian pyramid (the wavelet coefficients) compsed of images $h_1, h_2,\cdots$ as the difference of two consecutive Gaussian images. The inverse transform is the reconstruction of the image $f_0$ from the last Gaussian image $f_n$ (representing the approximation at the lowest scale level) and all Laplacian images $h_i$ ( $i=1,2,\cdots,n$) at different scale levels (representing details at different scale levels).

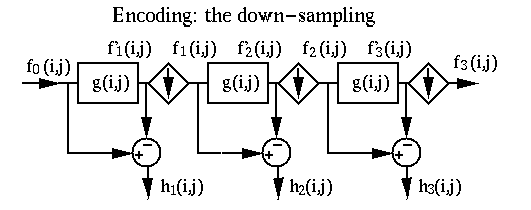
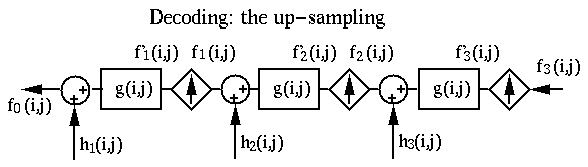
Similar to other orthogonal trnasforms (such as Fourier, discrete cosine, Walsh-Hardamard, etc.) and the Laplacian pyramid image coding, wavelet transform can also be used for signal/image compression and feature extraction.

It is in general much more effective to carry out compression in the transform domain as the signal is likely to be more decorrelated and the energy (information) more concentrated in a small number of components, compared to the original signal (in time or space domain), so that only a small subset of transform coefficients is needed to represent most of the information (energy) contained in the signal. This is the most essential reason why orthogonal transforms are widely used.

However, different from and usually better than other orthogonal transforms, the wavelet transform can represent information of the signal $x(t)$ in time (or space), such as the location or translation (represented by the subscript k of $\psi_{j,k}(t)$ for position), as well as in frequency, such as the different levels of details or resolution (represented by the subsript j for different scales). This added property makes it more likely that wavelet transform can represent a given signal more effecitvely and efficiently, in the sense that fewer number of coefficients than other transforms may be needed to approximate the signal.

For example, consider a time signal containing only an isolated narrow shape at some location $t=t_0$. In Fourier domain, this signal has a wide spectrum, i.e., a large number of frequency components are necessary to represent the signal. However, when wavelet transform is used, it is possible that a small number of coefficients associated with wavelet functions corresponding to the location of the shape in the signal can closely approximate (represent) the signal, thereby a high compression rate can be achieved.

Due to these advantages of wavelet transform compared to discrete fourier and discrete cosine transforms, it is used to replace the DCT in the image compression standard JPEG (1992) in the new version JPEG 2000.