Template Matching -- E186 Handout

Template matching is one of the simplest image detection methods. The idea is to slide an image template (binary shapes, or gray level patterns) over the image at hand - a 2D search - to see if an image object matching the template can be found somewhere in the image. The image template can be stored in the library as a 2D array $t(i,j)\;\;(i=-m/2, \cdots, m/2,\; j=-n/2, \cdots, n/2)$, where $m \times n$ is the size of the object.

Specifically, we define a distance between the template and a subimage

$$D(k,l)=\sum_{i=-m/2}^{m/2} \sum_{j=-n/2}^{n/2} [t(i,j)-f(k+i,l+j)]^2$$

where $M \times N$ is the size of the image, and $k=m/2, \cdots M-1-m/2$, $l=n/2, \cdots, N-1-n/2$. If the distance is smaller than a predetermined threshold

D(k,l) < T_d

then an object is said to be detected at location (k,l).

This distance can be written as

$$D(k,l) = \sum_{i=-m/2}^{m/2} \sum_{j=-n/2}^{n/2} [t^2(i,j)-2t(i,j)f(k+i,l+j)+f^2(k+i,l+j)]$$

The first term can be dropped as it only represents the energy contained in the template, independent of the image.

$$D(k,l) = \sum_{i=-m/2}^{m/2} \sum_{j=-n/2}^{n/2} [-2t(i,j)f(k+i,l+j)+f^2(k+i,l+j)]$$

The distance defined above should also be normalized by the total energy contained in the subimage to represent the relative difference between the template and the image, so that the distance is not affected by the subimage intensity. We redefine the distance as

$$\frac{\sum_i \sum_j [-2t(i,j)f(k+i,l+j)+f^2(k+i,l+j)]} {\sum_i \sum_j f^2(k+i,l+j)}$$ D(k,l) =

$$1-2\frac{\sum_i \sum_j t(i,j)f(k+i,l+j)} {\sum_i \sum_j f^2(k+i,l+j)}$$ =

We see that minimizing the distance is equivalent to maximizing the second term, the cross correlation between the template and the subimage:

$$R_{tf}(k,l)\stackrel{\triangle}{=} \frac{\sum_i \sum_j t(i,j)f(k+i,l+j)} {\sum_i \sum_j f^2(k+i,l+j)}$$

therefore the an object located at (k,l) is detected if the cross correlation is greater than another threshold T_r:

R_tf(k,l) > T_r

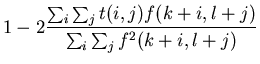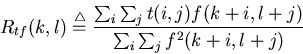
Rotational and size invariance can be achieved by extending the template match to a 4D to include two more dimensions for rotational angle $\phi$ and scaling factor s.