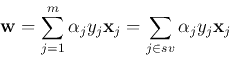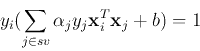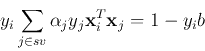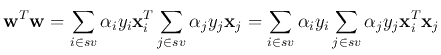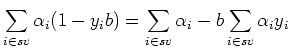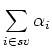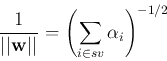Next: Soft Margin SVM
Up: Support Vector Machines (SVM)
Previous: The learning problem
For a decision hyper-plane
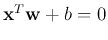 to separate the two
classes
to separate the two
classes
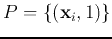 and
and
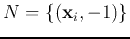 , it has to
satisfy
, it has to
satisfy
for both
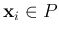 and
and
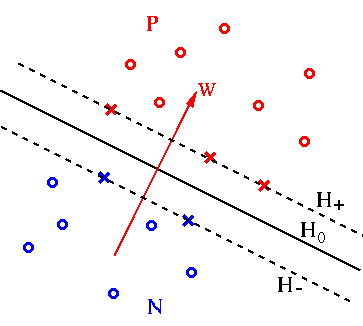
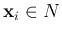 . Among all such planes
satisfying this condition, we want to find the optimal one
. Among all such planes
satisfying this condition, we want to find the optimal one 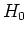 that
separates the two classes with the maximal margin (the distance between
the decision plane and the closest sample points).
that
separates the two classes with the maximal margin (the distance between
the decision plane and the closest sample points).
The optimal plane should be in the middle of the two classes, so that
the distance from the plane to the closest point on either side is the
same. We define two additional planes 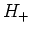 and
and 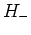 that are parallel
to
that are parallel
to 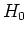 and go through the point closest to the plane on either side:
and go through the point closest to the plane on either side:
All points
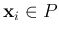 on the positive side should satisfy
on the positive side should satisfy
and all points
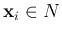 on the negative side should satisfy
on the negative side should satisfy
These can be combined into one inequality:
The equality holds for those points on the planes 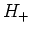 or
or 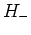 . Such
points are called support vectors, for which
. Such
points are called support vectors, for which
i.e., the following holds for all support vectors:
Moreover, the distances from the origin to the three parallel planes 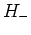 ,
,
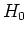 and
and 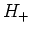 are, respectively,
are, respectively,
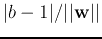 ,
,
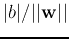 ,
and
,
and
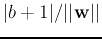 , and the distance between planes
, and the distance between planes 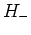 and
and 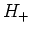 is
is
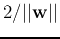 .
.
Our goal is to maximize this distance, or, equivalantly, to minimize the
norm 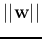 . Now the problem of finding the optimal decision plane
in terms of
. Now the problem of finding the optimal decision plane
in terms of 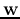 and
and 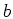 can be formulated as:
can be formulated as:
Since the objective function is quadratic, this constrained optimization
problem is called a quadratic program (QP) problem. (If the objective function
is linear instead, the problem is a linear program (LP) problem). This QP
problem can be solved by Lagrange multipliers method to minimize the following
with respect to 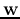 ,
, 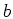 and the Lagrange coefficients
and the Lagrange coefficients 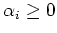
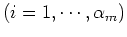 . We let
. We let
These lead, respectively, to
Substituting these two equations back into the expression of 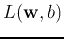 ,
we get the dual problem (with respect to
,
we get the dual problem (with respect to 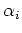 ) of the above
primal problem:
) of the above
primal problem:
The dual problem is related to the primal problem by:
i.e., 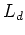 is the greatest lower bound (infimum) of
is the greatest lower bound (infimum) of 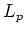 for all
for all 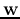 and
and 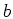 .
.
Solving this dual problem (an easier problem than the primal one), we get
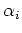 , from which
, from which 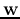 of the optimal plane can be found.
of the optimal plane can be found.
Those points 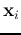 on either of the two planes
on either of the two planes 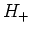 and
and 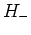 (for which
the equality
(for which
the equality
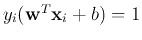 holds) are called support vectors
and they correspond to positive Lagrange multipliers
holds) are called support vectors
and they correspond to positive Lagrange multipliers 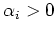 . The
training depends only on the support vectors, while all other samples away
from the planes
. The
training depends only on the support vectors, while all other samples away
from the planes 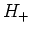 and
and 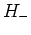 are not important.
are not important.
For a support vector 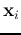 (on the
(on the 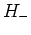 or
or 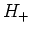 plane), the constraining
condition is
plane), the constraining
condition is
here 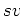 is a set of all indices of support vectors
is a set of all indices of support vectors 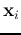 (corresponding
to
(corresponding
to 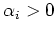 ). Substituting
). Substituting
we get
Note that the summation only contains terms corresponding to those support
vectors 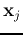 with
with 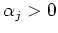 , i.e.
, i.e.
For the optimal weight vector 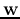 and optimal
and optimal 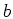 , we have:
, we have:
The last equality is due to
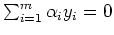 shown above.
Recall that the distance between the two margin planes
shown above.
Recall that the distance between the two margin planes 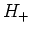 and
and 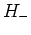 is
is
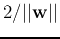 , and the margin, the distance between
, and the margin, the distance between 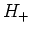 (or
(or 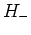 ) and the
optimal decision plane
) and the
optimal decision plane 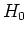 , is
, is



Next: Soft Margin SVM
Up: Support Vector Machines (SVM)
Previous: The learning problem
Ruye Wang
2016-08-19
![]() to separate the two
classes
to separate the two
classes
![]() and
and
![]() , it has to
satisfy
, it has to
satisfy
![]() and
and ![]() that are parallel
to
that are parallel
to ![]() and go through the point closest to the plane on either side:
and go through the point closest to the plane on either side:
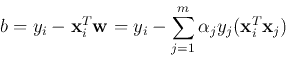
![]() ,
,
![]() and
and ![]() are, respectively,
are, respectively,
![]() ,
,
![]() ,
and
,
and
![]() , and the distance between planes
, and the distance between planes ![]() and
and ![]() is
is
![]() .
.

![]() . Now the problem of finding the optimal decision plane
in terms of
. Now the problem of finding the optimal decision plane
in terms of ![]() and
and ![]() can be formulated as:
can be formulated as:
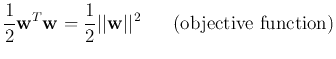
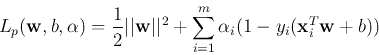
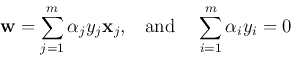
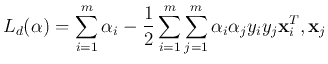
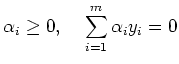
![]() , from which
, from which ![]() of the optimal plane can be found.
of the optimal plane can be found.
![]() on either of the two planes
on either of the two planes ![]() and
and ![]() (for which
the equality
(for which
the equality
![]() holds) are called support vectors
and they correspond to positive Lagrange multipliers
holds) are called support vectors
and they correspond to positive Lagrange multipliers ![]() . The
training depends only on the support vectors, while all other samples away
from the planes
. The
training depends only on the support vectors, while all other samples away
from the planes ![]() and
and ![]() are not important.
are not important.
![]() (on the
(on the ![]() or
or ![]() plane), the constraining
condition is
plane), the constraining
condition is