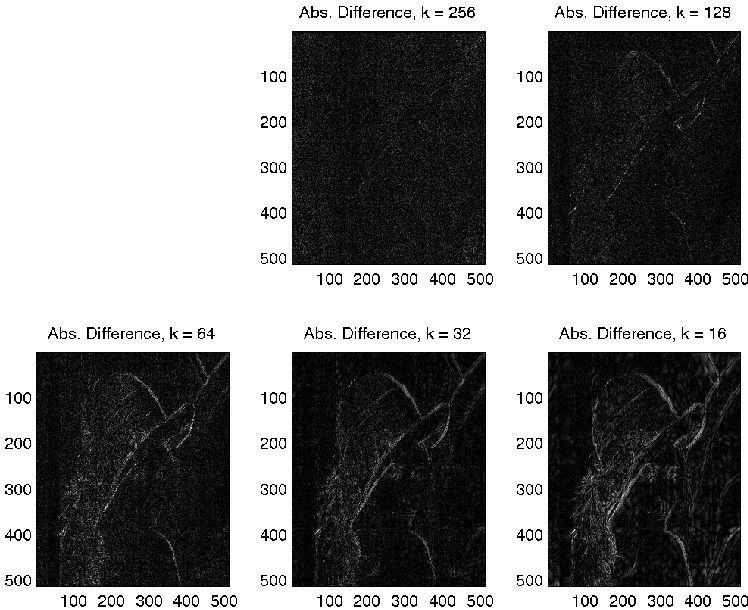
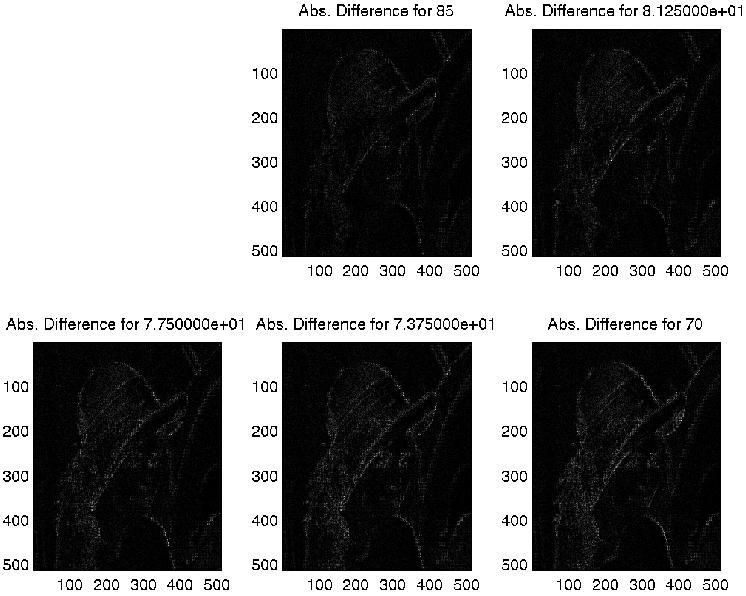
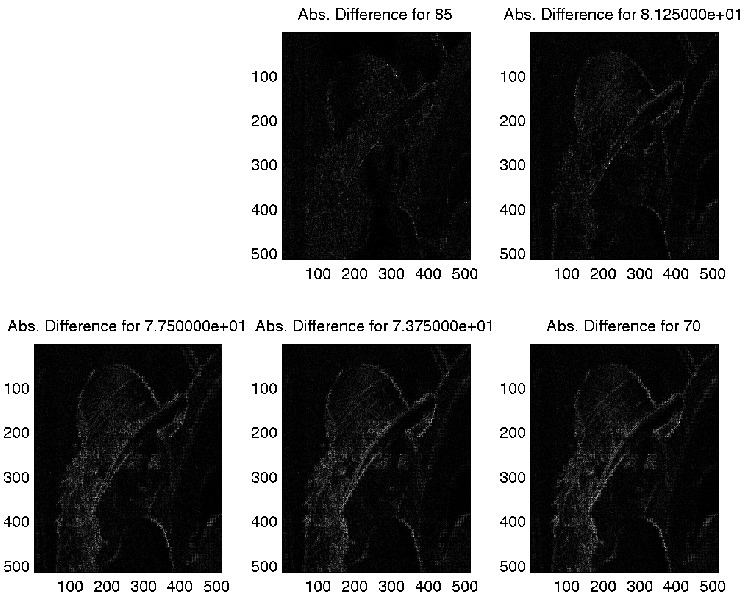
Figure 2. The absolute difference between the original and the re-constructed images.
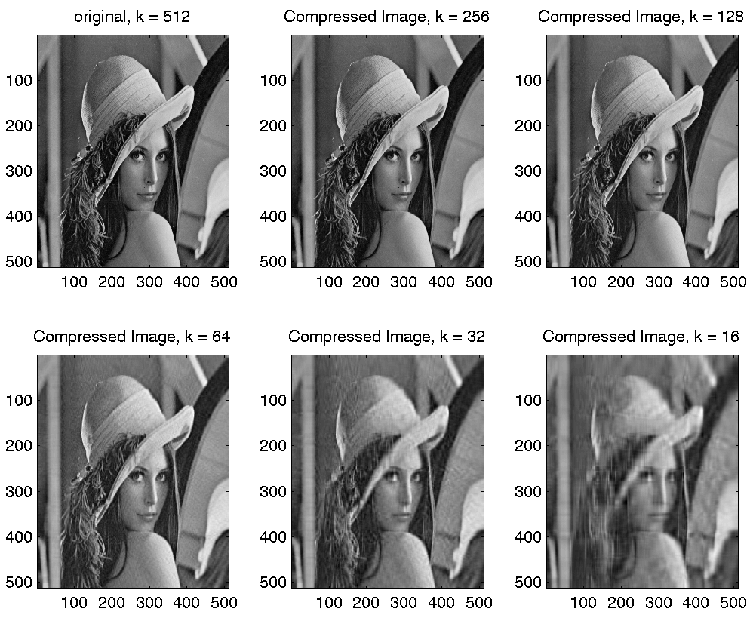
Original Image: A = USVH, where U is m by n, V is n by n, and S = diag(r1, r2,...,rk,0,...,0) Re-constructed Image: A1 = US1VH, where U is m by k1, V is k1 by n, and S1 = diag(r1, r2,...,rk1) and ||A - A1||2 = rk1 + 1
PSNR = 10 log10((max. range)2 / Root Mean Square Error )


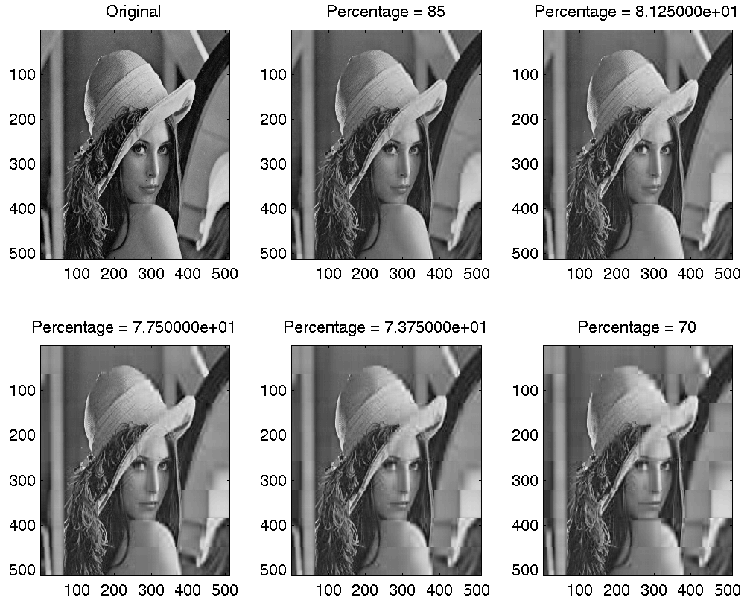
Rank k1 used for each sub-block: (r1+r2+...+rk1) Specified Percentage =------------------ (r1+r2+...+rk)
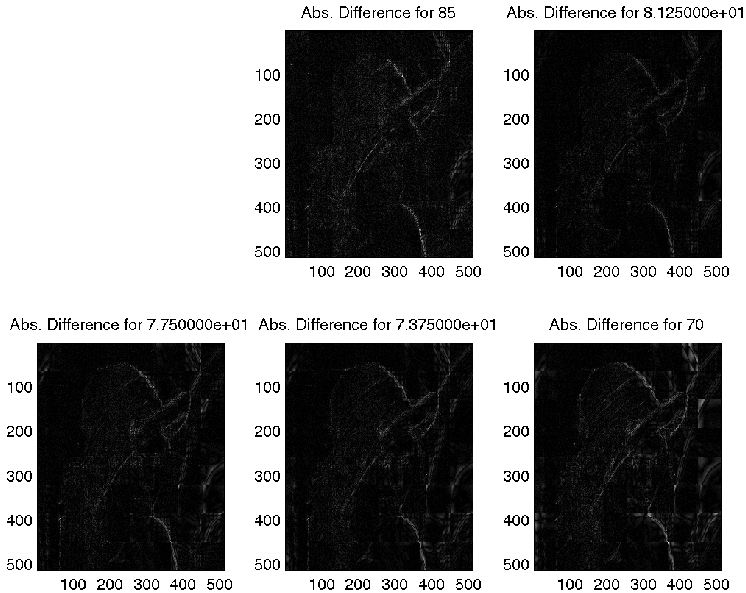
Ranks used for percentage = 7.750000e+01:
RUsed =
1 5 2 4 3 1 3 8
2 7 10 8 4 5 6 7
1 5 12 10 6 5 7 2
1 6 11 13 5 8 5 1
2 12 15 11 4 8 3 2
2 14 13 9 5 8 1 1
3 14 13 11 2 6 3 4
3 15 15 6 1 3 4 7
Ranks used for percentage = 70:
RUsed =
1 1 1 2 2 1 2 5
1 2 5 4 3 3 4 5
1 3 7 6 3 3 5 1
1 3 8 9 3 5 3 1
1 9 12 8 3 5 2 1
1 10 10 5 3 5 1 1
2 11 10 6 1 4 2 3
2 10 12 4 1 2 3 5
64-by-64 block-size:
===> Percentage of Singular | Average Ranks | Avg. Percentage of
Values Sum Used Ranks Used.
85 10.500000 0.164062
81.25 7.968750 0.124512
77.5 6.156250 0.096191
73.75 4.937500 0.077148
70 4.046875 0.063232
8-by-8 block-size:
===> Percentage of Singular | Average Ranks | Avg. Percentage of
Values Sum Used Ranks Used.
85 1.540039 0.192505
81.25 1.371582 0.171448
77.5 1.256104 0.157013
73.75 1.176514 0.147064
70 1.115234 0.139404
Original Image: A - mean = USVH, where U is m by n, V is n by n, and S = diag(r1, r2,...,rk,0,...,0) Re-constructed Image: A1 = US1VH + mean, where U is m by k1, V is k1 by n, and S1 = diag(r1, r2,...,rk1)
8-by-8 block-size:
===> Percentage of Singular | Average Ranks | Avg. Percentage of
Values Sum Used Ranks Used.
85 2.311279 0.288910
81.25 1.371582 0.171448
77.5 1.015137 0.126892
73.75 1.000000 0.125000
70 1.000000 0.125000
m = 0.3884 <---- mean
% function SDVCompression_3(F, BlockSize, SP, EP)
% Image Compression, take out the mean
%
%
% F: input file, a 2-D array
% BlockSize: 64, 32, 16, 8
% SP: Staring percentage of singular values AREA used
% EP: Ending percentage of singular values AREA used
% SP < EP
%
%
% testing my idea of using cumulative singularvalues
%
% James Chen, 11/30/2000
% ECS 289K, Project
%
close all
if (SP > EP)
disp('SP must be smaller than EP!!!')
return
end
% read in the image
IMG1 = imread(F);
X1org = im2double(IMG1);
XSize = size(X1org);
figure(1);
colormap(gray);
imagesc(X1org);
title (sprintf('Original Image: %s, Size: %i x %i', F, XSize(1), XSize(2)));
% mean
m = mean(mean(X1org))
X1org = X1org - m;
% display the image
figure(2);
subplot(2,3,1);
% shown in original size: imshow(X1org);
% or: in matrix format:
colormap(gray);
imagesc(X1org+m);
%title ('Original');
NumBlocks = XSize(1)/BlockSize;
PercentageStep = (EP - SP)/4.0;
Percentage = EP;
pl = 2;
while (pl <= 6)
for i = 1:NumBlocks
r = (i-1) * BlockSize + 1;
for j = 1:NumBlocks
%disp(sprintf('Processing block %i %i', i,j))
c = (j-1) * BlockSize + 1;
TB = X1org(r:r+BlockSize-1, c: c+BlockSize-1);
[TU,TS,TV] = svd(TB);
%U(i, j, :, :) = TU;
%S(i, j, :, :) = TS;
%V(i, j, :, :) = TV;
SV = diag(TS); % a n by 1 vector
% cumulative sum of singular values
s = size(SV);
R(i,j) = s(1);
% rank for original block
TCS(1) = SV(1);
for k = 2: s(1)
TCS(k) = TCS(k-1) + SV(k);
end
%CS(i,j,:,:) = TCS;
%
% reconstruction, de-compression
%
v = TCS(s(1)) * Percentage *0.01;
% find the rank used for each block
rr = 1;
k = s(1)-1;
while (k >=1)
if ( (TCS(k) <= v) & (TCS(k+1) >= v))
rr = k+1;
break;
end;
k = k-1;
end
RUsed(i,j) = rr;
PRUsed(i,j) = rr/s(1);
%disp(sprintf('rank used = %i', rr))
X = TU(:, 1:rr) * TS(1:rr, 1:rr) * TV(:, 1:rr)';
CI(r:r+BlockSize-1, c: c+BlockSize-1) = X;
end
end
% add the mean back to image
CI = CI + m;
disp('--------------')
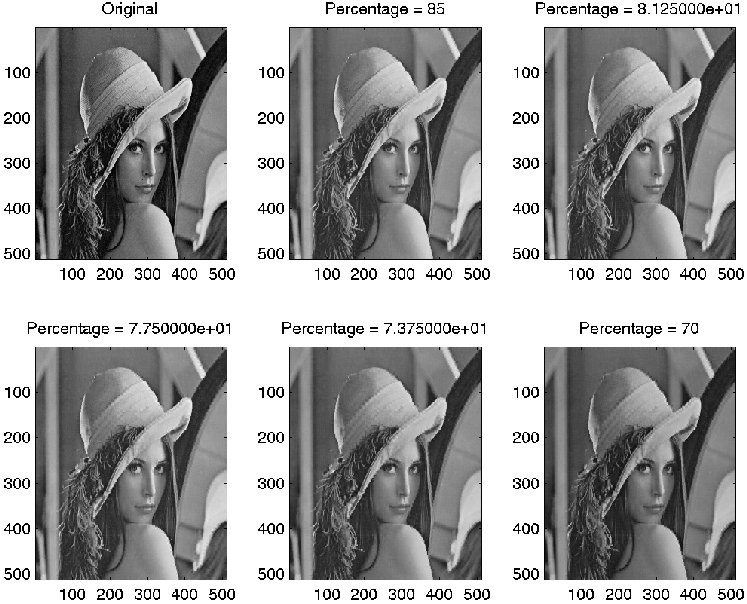
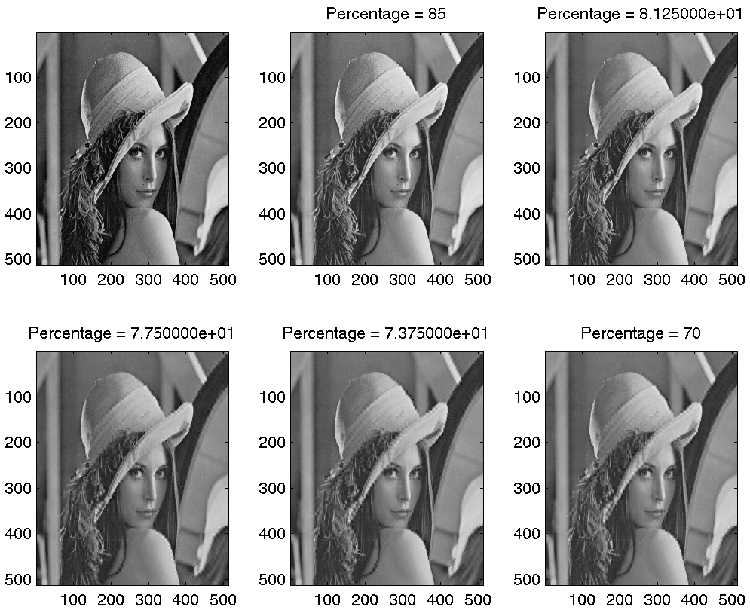
disp(sprintf('Rnaks used for percentage = %i:\n', Percentage))
RUsed
avg = sum(sum(RUsed))/(NumBlocks*NumBlocks);
disp(sprintf('Average ranks used = %f\n\n', avg))
disp(sprintf('Ranks used / %i:', s(1)))
PRUsed
avg = sum(sum(PRUsed))/(NumBlocks*NumBlocks);
disp(sprintf('Average percentage of ranks used = %f\n', avg))
%display
figure(2)
subplot(2,3, pl);
colormap(gray);
imagesc(CI);
title(sprintf('Percentage = %i', Percentage))
% !!!! add th emean back to the original picture
X1org = X1org + m;
Diff = X1org - CI;
figure(3)
subplot(2,3, pl);
colormap(gray);
imagesc(Diff);
title(sprintf('Difference for %i', Percentage))
figure(4)
subplot(2,3, pl);
colormap(gray);
imagesc(abs(Diff));
title(sprintf('Abs. Difference for %i', Percentage))
%figure(5)
%subplot(2,3,pl)
%bar(RUsed)
%title('Ranks used for each sub-block');
%axis([0 NumBlocks+1 0 s(1)]);
%figure(6)
%subplot(2,3,pl)
%bar(PRUsed)
%title('Percentage of the ranks used');
%axis([0 NumBlocks+1 0 1]);
Percentage = Percentage - PercentageStep;
pl = pl + 1;
% compute Peak SN ratio:
mse1 = 0;
for i = 1: XSize(1)
for j = 1: XSize(2)
mse1 = mse1 + Diff(i,j)*Diff(i,j);
end
end
mse1 = mse1 /(XSize(1) * XSize(2));
mse1 = sqrt(mse1)
PSNR = 10 * log10(255^2/mse1)
end