Arbitrary resizing

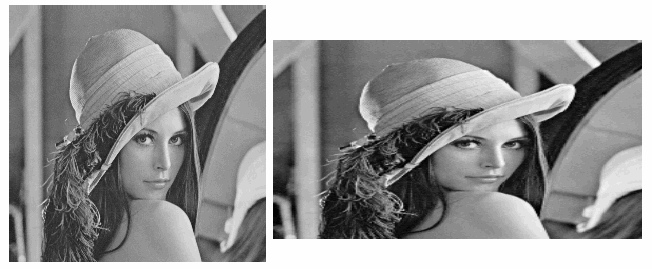
It is obviously more desirable to arbitrarily resize a given image (enlarge or reduce the image proportionally or non-proportionally). We first consider converting a one-dimensional m-sample input $\{ x_i, (i=0, 1, \cdots, m-1) \}$ into an n-sample output $\{ y_j, (j=0, 1, \cdots, n-1) \}$, where $n$ is the desired size of the output, which may be either smaller or greater than $m$, i.e., the scaling factor $n/m$ can be either greater or smaller than 1 (for either enlargement or reduction). The method is essentially a two-step process of linear interpolation and re-sampling.

• Convert indices:

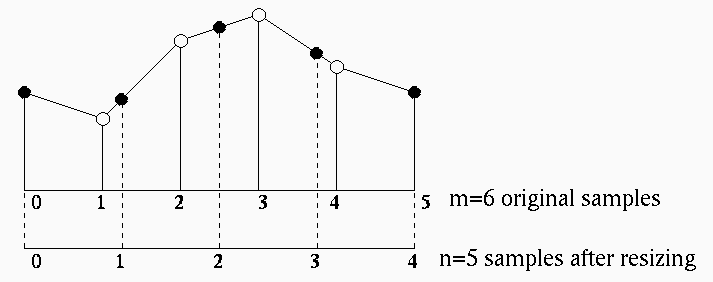
  Represent each index $0 \leq k \leq n-1$ of the output as a floating point number $p$ in the range of $0 \leq i \leq m-1$ of the input indices:

  $$\frac{p}{m-1}=\frac{k}{n-1},\;\;\;\;\; \;\;\;\; p=k\; \frac{m-1}{n-1}$$ (14)

  The indices of the two neighboring samples of $p$ can be found as

  $$i = \lfloor p \rfloor \;\;\leq\;\; p \;\;\leq \;\;\lceil p \rceil =i+1$$ (15)

  where $\lfloor p \rfloor$ and $\lceil p \rceil$ represent, respectively, the floor and the ceiling of $p$, i.e., the largest integer smaller than $p$ and the smallest integer larger than $p$.

• Interpolate (Re-sampling):

  Find the fraction $0 \leq (u=p-i) \leq 1$ and $d$ as shown in the figure:

  $$\frac{d}{u}=\frac{x_{i+1}-x_{i}}{(i+1)-i}=x_{i+1}-x_i, \;\;\;\; \;\;\;\;\;\;d=u(x_{i+1}-x_i)$$ (16)

  Now the kth value $y_k$ of the output can be found as the interpolation between $x_i$ and $x_{i+1}$:

  $$y_k=x_{p}=x_i+d=x_i+u(x_{i+1}-x_i)$$ (17)

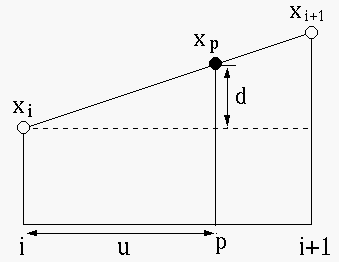
This method of linear interpolation can be generalized from 1-D to 2-D bilinear interpolation for image resizing.

• Convert indices:

  Similar to the 1D case, we first convert the integer indices $(k,l)$ of each pixel of the output image of the desired size into real coordinates $(p, q)$ in the range of the input image. Then the corresponding fractions $u$ and $v$ in both horizontal and vertical dimensions can be found:

  $$i = \lfloor p \rfloor, \;\;\;\;\; i+1=\lceil p \rceil, \;\;\;\;\; u=p-i$$ (18)

  $$j = \lfloor q \rfloor, \;\;\;\;\; j+1=\lceil q \rceil, \;\;\;\;\; v=q-j$$ (19)

• Interpolate:

  Find value $x[p,q]$ as the bilinear interpolation of its four immediate neighbors in the input image, represented by

  $$a=x_{i,j},\;\;\;\;\;\; b=x_{i+1,j},\;\;\;\;\;\; c=x_{i,j+1},\;\;\;\;\;\; d=x_{i+1,j+1}$$ (20)

  

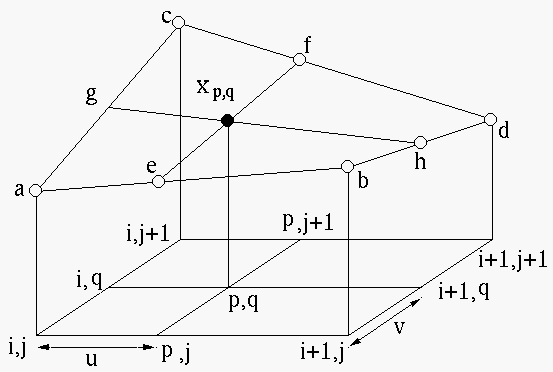
  The bilinear interpolation is carried out in two levels of linear interpolations. We first find the two interpolations of $a$, $b$ and $c$, $d$ along the dimension with index $i$:

  $$\left\{ \begin{array}{ll} e=a+u(b-a) \\ f=c+u(d-c) \end{array} \right.$$ (21)

  and then find $y[k,l]=x[p,q]$ as the linear interpolation of e and f along the dimension with index $j$:

  $$y[k,l]=x[p,q]=e+v(f-e)=(1-u-v+uv)a+u(1-v)b+v(1-u)c+uvd$$ (22)

  Alternatively and equivalently, we could first find the interpolations along the dimension in $j$:

  $$\left\{ \begin{array}{ll} g=a+v(c-a) \\ h=b+v(d-b) \end{array} \right.$$ (23)

  and then find the pixel value of the output as the interpolation along the dimension in $i$:

  $$y[k,l]=x[p,q]=g+u(h-g)=(1-u-v+uv)a+u(1-v)b+v(1-u)c+uvd$$ (24)

  The result is exactly the same as before.