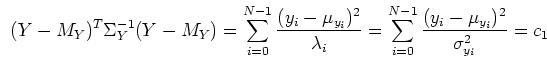Next: About this document ...
Up: pca
Previous: Comparison with Other Orthogonal
Assume the 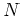 random variables in
random variables in
![$X=[x_0,\cdots, x_{N-1}]^T$](img122.png) have a normal
joint probability density function:
have a normal
joint probability density function:
where 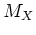 and
and 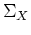 are the mean vector and covariance matrix of
are the mean vector and covariance matrix of 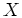 ,
respectively. When
,
respectively. When 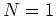 ,
, 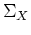 and
and 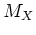 become
become 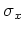 and
and 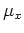 ,
respectively, and the density function becomes single variable normal
distribution.
,
respectively, and the density function becomes single variable normal
distribution.
The shape of this normal distribution in the N-dimensional space can be
found by considering the iso-value hyper-surface in the space determined by
equation
where 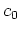 is a constant. Or, equivalently, this equation can be written as
is a constant. Or, equivalently, this equation can be written as
where 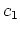 is another constant related to
is another constant related to 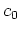 ,
, 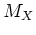 and
and 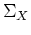 .
In particular, with
.
In particular, with 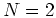 variables
variables 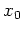 and
and 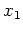 , we have
, we have
Here we have assumed
The above quadratic equation represents an ellipse (instead of any other
quadratic curve) centered at
![$M_X=[\mu_{x_0}, \mu_{x_1}]^T$](img139.png) , because
, because 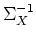 ,
as well as
,
as well as 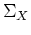 , is positive definite:
, is positive definite:
When 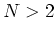 , the equation
, the equation
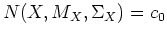 represents a hyper
ellipsoid in the N-dimensional space. The center and spatial distribution of
this ellipsoid are determined by
represents a hyper
ellipsoid in the N-dimensional space. The center and spatial distribution of
this ellipsoid are determined by 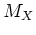 and
and 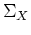 , respectively.
, respectively.
When
![$X=[x_0,\cdots, x_{N-1}]^T$](img122.png) is completely decorrelated by KLT:
is completely decorrelated by KLT:
the covariance matrix becomes diagonalized:
and equation
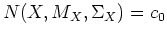 becomes
becomes
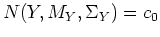 , or
, or
This equation represents a standard ellipsoid in the N-dimensional space.
In other words, KLT 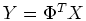 rotates the coordinate system so that the
ellipsoid associated with the normal distribution of
rotates the coordinate system so that the
ellipsoid associated with the normal distribution of 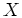 becomes a standardized
ellipsoid associated with the normal distribution of
becomes a standardized
ellipsoid associated with the normal distribution of 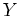 , whose axes are
parallel to
, whose axes are
parallel to 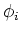 (
(
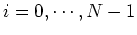 ), the axes of the new coordinate
system, with the corresponding semi axes equal to
), the axes of the new coordinate
system, with the corresponding semi axes equal to
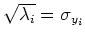 .
.
The standardization of the ellipsoid is the essential reason why KLT has the two
desirable properties: (a) decorrelation and (b) compaction of energy, as illustrated
in the figure:




Next: About this document ...
Up: pca
Previous: Comparison with Other Orthogonal
Ruye Wang
2004-09-29
![]() random variables in
random variables in
![]() have a normal
joint probability density function:
have a normal
joint probability density function:
![\begin{displaymath}p(x_0,\cdots, x_{N-1})=N(X, M_X, \Sigma_X)=
\frac{1}{(2\pi)^...
...t\vert^{1/2}}
exp[ -\frac{1}{2}(X-M_X)^T\Sigma_X^{-1}(X-M_X)] \end{displaymath}](img123.png)
![$\displaystyle [x_0-\mu_{x_0}, x_1-\mu_{x_1}]
\left[ \begin{array}{cc} a & b/2 \...
...ht]
\left[ \begin{array}{c} x_0-\mu_{x_0} x_1-\mu_{x_1} \end{array} \right]$](img136.png)
![\begin{displaymath}
\Sigma_X^{-1}=\left[ \begin{array}{cc} a & b/2 b/2 & c \end{array} \right]
\end{displaymath}](img138.png)
![]() , because
, because ![]() ,
as well as
,
as well as ![]() , is positive definite:
, is positive definite:
![]() , the equation
, the equation
![]() represents a hyper
ellipsoid in the N-dimensional space. The center and spatial distribution of
this ellipsoid are determined by
represents a hyper
ellipsoid in the N-dimensional space. The center and spatial distribution of
this ellipsoid are determined by ![]() and
and ![]() , respectively.
, respectively.
![]() is completely decorrelated by KLT:
is completely decorrelated by KLT:
![\begin{displaymath}
\Sigma_Y =\Lambda=
\left[ \begin{array}{cccc}
\lambda_0 & ...
...s \\
0 & 0 & \cdots & \sigma^2_{y_{N-1}} \end{array} \right]
\end{displaymath}](img145.png)