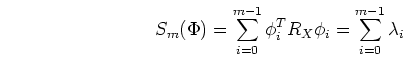Next: Comparison with Other Orthogonal
Up: pca
Previous: KLT Completely Decorrelates the
Consider a general orthogonal transform pair defined as
where 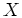 and
and 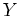 are N by 1 vectors and
are N by 1 vectors and 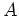 is an arbitrary N by N orthogonal
matrix
is an arbitrary N by N orthogonal
matrix 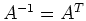 .
.
We represent 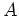 by its column vectors
by its column vectors
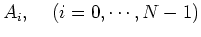 as
as
or
Now the ith component of 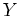 can be written as
can be written as
As we assume the mean vector of 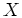 is zero
is zero 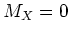 (and obviously we also have
(and obviously we also have
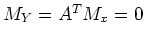 ), we have
), we have 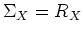 , and the variance of the ith element in both
, and the variance of the ith element in both
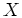 and
and 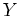 are
are
and
where
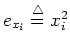 and
and
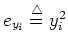 represent the energy contained in the
ith component of
represent the energy contained in the
ith component of 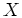 and
and 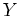 , respectively. In order words, the trace of
, respectively. In order words, the trace of
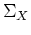 (the sum of all the diagonal elements of the matrix) represents the
expectation of the total amount of energy contained in the signal
(the sum of all the diagonal elements of the matrix) represents the
expectation of the total amount of energy contained in the signal 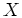
Since an orthogonal transform 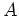 does not change the length of a vector X,
i.e.,
does not change the length of a vector X,
i.e.,
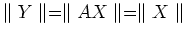 ,
where
,
where
the total energy contained in the signal vector 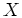 is conserved after the
orthogonal transform.
(This conclusion can also be obtained from the fact that orthogonal transforms
do not change the trace of a matrix.)
is conserved after the
orthogonal transform.
(This conclusion can also be obtained from the fact that orthogonal transforms
do not change the trace of a matrix.)
We next define
where 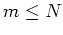 .
. 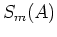 is a function of the transform matrix
is a function of the transform matrix 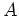 and
represents the amount of energy contained in the first
and
represents the amount of energy contained in the first 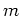 components of
components of 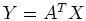 .
Since the total energy is conserved,
.
Since the total energy is conserved, 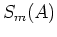 also represents the percentage
of energy contained in the first
also represents the percentage
of energy contained in the first 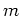 components. In the following we will
show that
components. In the following we will
show that 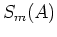 is maximized if and only if the transform
is maximized if and only if the transform 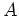 is the
KLT:
is the
KLT:
i.e., KLT optimally compacts energy into a few components of the signal.
Consider
Now we need to find a transform matrix 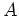 so that
so that
The constraint 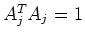 is to guarantee that the column vectors in
is to guarantee that the column vectors in 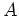 are normalized. This constrained optimization problem can be solved by Lagrange
multiplier method as shown below.
are normalized. This constrained optimization problem can be solved by Lagrange
multiplier method as shown below.
We let
(* the last equal sign is due to explanation in the handout of review of
linear algebra.)
We see that the column vectors of 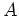 must be the eigenvectors of
must be the eigenvectors of
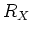 :
:
i.e., the transform matrix must be
Thus we have proved that the optimal transform is indeed KLT, and
where the ith eigenvalue 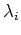 of
of 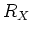 is also the average (expectation)
energy contained in the ith component of the signal.
If we choose those
is also the average (expectation)
energy contained in the ith component of the signal.
If we choose those 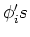 that correspond to the
that correspond to the 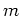 largest eigenvalues of
largest eigenvalues of
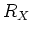 :
:
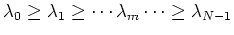 ,
then
,
then 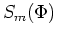 will achieve maximum.
will achieve maximum.



Next: Comparison with Other Orthogonal
Up: pca
Previous: KLT Completely Decorrelates the
Ruye Wang
2004-09-29


![]() by its column vectors
by its column vectors
![]() as
as
![\begin{displaymath}A^{T}=\left[ \begin{array}{c} A_0^{T} . . A_{N-1}^{T} \end{array} \right]
\end{displaymath}](img84.png)
![]() is zero
is zero ![]() (and obviously we also have
(and obviously we also have
![]() ), we have
), we have ![]() , and the variance of the ith element in both
, and the variance of the ith element in both
![]() and
and ![]() are
are
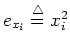 and
and
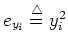 represent the energy contained in the
ith component of
represent the energy contained in the
ith component of 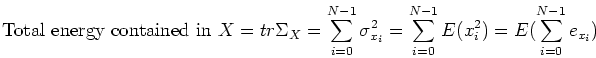
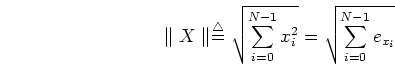
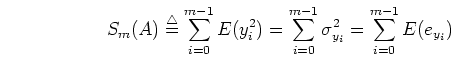
![$\displaystyle \sum_{i=0}^{m-1} E(y_i^2)=
\sum_{i=0}^{m-1} E[A_i^{T}X (A_i^{T}X)^{T}]$](img102.png)
![$\displaystyle \sum_{i=0}^{m-1} E[A_i^{T}X (X^{T}A_i)]
=\sum_{i=0}^{m-1} A_i^{T}E(X X^{T})A_i$](img103.png)
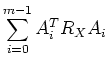
![]() so that
so that
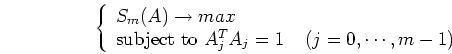
![$\displaystyle \frac{\partial}{\partial A_i}[S_m(A)-\sum_{j=0}^{m-1}
\lambda_j(A_j^{T}A_j-1) ]=0$](img107.png)
![$\displaystyle \frac{\partial}{\partial A_i}[\sum_{j=0}^{m-1}
(A_j^{T}R_XA_j-\lambda_j A_j^{T}A_j+\lambda_j) ]$](img108.png)
![$\displaystyle \frac{\partial}{\partial A_i}
[A_i^{T}R_XA_i-\lambda_i A_i^{T}A_i ]$](img109.png)