Next: About this document ...
Up: MCMC
Previous: Appendix C: Matrix Operations
Let
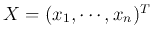 is an n-dimensional random vector with
mean vector and covariance matrix:
is an n-dimensional random vector with
mean vector and covariance matrix:
A linear transform of 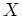 can be defined by an m by n matrix
can be defined by an m by n matrix 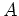 and
the result
and
the result 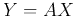 is an m-dimensional random vector with the mean
vector and covariance matrix:
is an m-dimensional random vector with the mean
vector and covariance matrix:
In particular, if 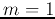 ,
,
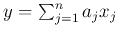 is a linear combination of
is a linear combination of
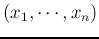 and its mean is
and its mean is
and its variance is
If
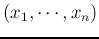 are independent, i.e.,
are independent, i.e., 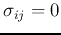 for
for 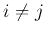 ,
then
,
then
Ruye Wang
2018-03-26
![]() is an n-dimensional random vector with
mean vector and covariance matrix:
is an n-dimensional random vector with
mean vector and covariance matrix:
![\begin{displaymath}\Sigma_x=E(X-M_x)(X-M_x)^T=E (XX^T)-M_x M_x^T
=\left[ \begin{...
.....&...\\ \sigma_{n1}^2 &...&\sigma_{nn}^2 \end{array} \right]
\end{displaymath}](img194.png)
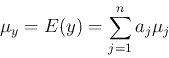
![\begin{displaymath}\sigma^2_y=A\Sigma_x A^T=[a_1,\cdots,a_n]
\left[\begin{array...
...rray} \right]=\sum_{i=1}^n \sum_{j=1}^n a_i a_j
\sigma_{ij}^2
\end{displaymath}](img204.png)