Given a set of ![]() sample points
sample points
![]() of an
unknown continuous function
of an
unknown continuous function ![]() , we want to estimate the derivative
, we want to estimate the derivative ![]() of the function at an arbitrary point
of the function at an arbitrary point ![]() . In general, the sample points are not
assumed to be evenly spaced in the dimension of
. In general, the sample points are not
assumed to be evenly spaced in the dimension of ![]() .
.
We first reconstruct a continuous function to fit a set of n+1 sample points around the
point ![]() for which the derivative
for which the derivative ![]() needs to be estimated by Lagrange interpolation:
needs to be estimated by Lagrange interpolation:
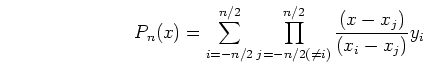
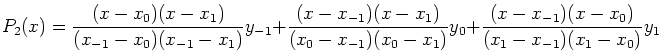
When
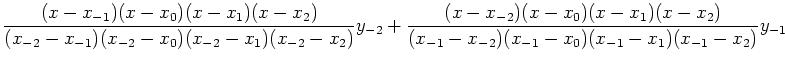 |
|||
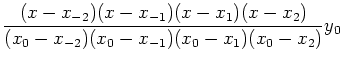 |
|||
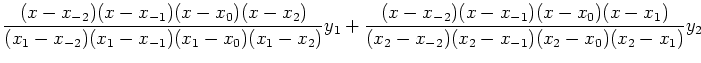 |
Now the derivative of function ![]() at any point
at any point ![]() can be estimated by
differentiating
can be estimated by
differentiating ![]() . For example, when
. For example, when ![]() :
:
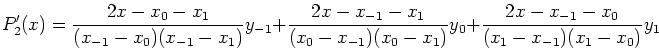
In particular, when the point
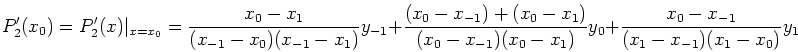
When
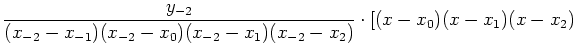 |
|||
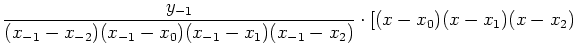 |
|||
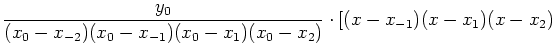 |
|||
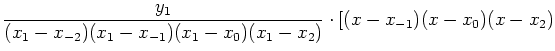 |
|||
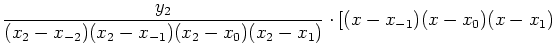 |
|||
When
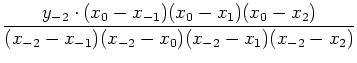 |
|||
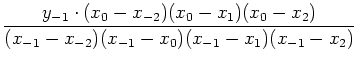 |
|||
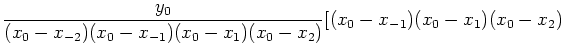 |
|||
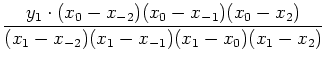 |
|||
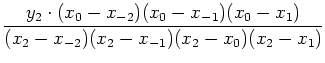 |
In particular when ![]() 's are equally spaced, i.e.
's are equally spaced, i.e. ![]() , the
estimated derivative at
, the
estimated derivative at ![]() can be found to be
can be found to be
It can be shown that the error is
We can also get backward estimation of ![]() using
using
![]() :
:
The average of the forward and backward estimations can be used as the final
estimation of ![]() .
.
To overcome possible noise, better estimation may be obtained by using more points, such as 4 or 5 points.
The four-point forward estimation:
The four-point forward estimation:
The five-point forward estimation:
The five-point backward estimation:
This method is based on the assumption that the function ![]() is
continuous and noise-free. If this is not the case, the estimation error
could be large.
is
continuous and noise-free. If this is not the case, the estimation error
could be large.