


Next: Restoration by Inverse Filtering
Up: motion
Previous: motion
The general process of image acquisition (e.g., taking an image by a camera) can be
modeled by
where 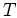 is the exposure time,
is the exposure time, 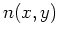 is some additive noise, and
is some additive noise, and
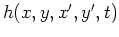 is a function characterizing the distortion introduced by the imaging system, caused
by, for example, limited aperture, out of focus, random atmospheric turbulence,
and/or relative motion. If the imaging system is ideal, spatial and time invariant,
and noise-free, i.e.,
is a function characterizing the distortion introduced by the imaging system, caused
by, for example, limited aperture, out of focus, random atmospheric turbulence,
and/or relative motion. If the imaging system is ideal, spatial and time invariant,
and noise-free, i.e.,
then the equation above for the imaging process becomes
If the signal is also time invariant (a stationary scene), i.e.,
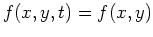 ,
the image obtained is simply
,
the image obtained is simply
However, if there exists some relative planar motion (only in the x-y plane) between
the object and the camera system, i.e., the signal 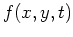 is no longer time
invariant. This planar motion can be described by its two components in
is no longer time
invariant. This planar motion can be described by its two components in 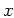 and
and
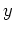 directions
directions
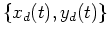 , and the image of this moving object becomes
, and the image of this moving object becomes
For simplicity, we assume a 1-D linear motion of velocity 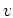 in
in 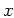 direction
only:
direction
only:
We introduce a new variable 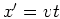 , we have
, we have 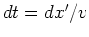 , the integral from
, the integral from 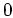 to
to 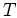 with respect to
with respect to 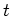 becomes integral from
becomes integral from 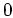 to
to 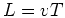 with respect to
with respect to
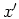 , the equation for the imaging process becomes
, the equation for the imaging process becomes
where 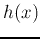 is the impulse response function of the imaging system
is the impulse response function of the imaging system
which is a square impulse. Note that variable 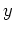 can be treated as a parameter
and in this case motion restoration is essentially a 1-D problem.
can be treated as a parameter
and in this case motion restoration is essentially a 1-D problem.
If the linear motion is not in either 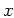 or
or 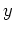 direction, we can rotate the
image so that the motion direction is aligned with one of the axes after the
rotation and modeled by the equation above.
direction, we can rotate the
image so that the motion direction is aligned with one of the axes after the
rotation and modeled by the equation above.




Next: Restoration by Inverse Filtering
Up: motion
Previous: motion
Ruye Wang
2013-11-18
![]() is no longer time
invariant. This planar motion can be described by its two components in
is no longer time
invariant. This planar motion can be described by its two components in ![]() and
and
![]() directions
directions
![]() , and the image of this moving object becomes
, and the image of this moving object becomes
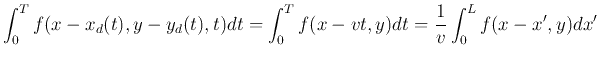
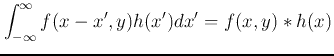
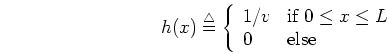
![]() or
or ![]() direction, we can rotate the
image so that the motion direction is aligned with one of the axes after the
rotation and modeled by the equation above.
direction, we can rotate the
image so that the motion direction is aligned with one of the axes after the
rotation and modeled by the equation above.
