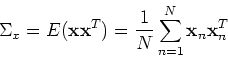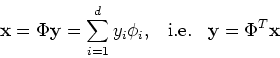Next: Mapping to high dimensional
Up: Kernel PCA (KPCA)
Previous: Kernel PCA (KPCA)
The main idea of principal component analysis (PCA) is to represent the given
data points
![${\bf x}=[x_1,\cdots,x_d]^T$](img1.png) in a possibly high d-dimensional
space into a space spanned by the eigenvectors of the covariance matrix
in a possibly high d-dimensional
space into a space spanned by the eigenvectors of the covariance matrix
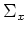 of the data points. In the new space the different dimensions
(the principal components) of the data points are totally de-correlated and
the energy contained in the data, in terms of the sum of the variances in
all dimensions, is optimally compacked into a small number of components,
so that a large number of components can be discarded without losing much
information in the data, i.e., the dimensionality of the space can be much
reduced.
of the data points. In the new space the different dimensions
(the principal components) of the data points are totally de-correlated and
the energy contained in the data, in terms of the sum of the variances in
all dimensions, is optimally compacked into a small number of components,
so that a large number of components can be discarded without losing much
information in the data, i.e., the dimensionality of the space can be much
reduced.
Without loss of generality, we assume the data points have zero mean
and the  covariance matrix can be estimated by
covariance matrix can be estimated by
We then find the eigenvector 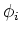 corresponding to the i-th eigenvalue
corresponding to the i-th eigenvalue
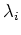 for all
for all 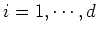 :
:
where the eigenvalues are assumed to be in decreasing order:
A 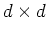 matrix can be constructed by the eigenvectors as
matrix can be constructed by the eigenvectors as
and we have
where
Since 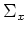 is symmectric, its eigenvectors
is symmectric, its eigenvectors 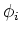 are orthogonal to
each other
are orthogonal to
each other
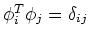 and
and
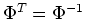 is orthogonal.
Now we have
is orthogonal.
Now we have
Now all data points 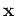 can be mapped to a new space spanned by
can be mapped to a new space spanned by
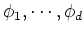 :
:
The i-th component of
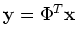 is the projection of
is the projection of
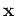 on the i-th axis
on the i-th axis 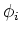 :
:
The covariance matrix in this space is
i.e., all components in the new space are de-correlated:
By using only the first few components in 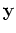 , we can reduce the
dimensionality of the data without losing much of the energy (information)
in terms of the sum of the variances in the
, we can reduce the
dimensionality of the data without losing much of the energy (information)
in terms of the sum of the variances in the 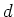 components.
components.



Next: Mapping to high dimensional
Up: Kernel PCA (KPCA)
Previous: Kernel PCA (KPCA)
Ruye Wang
2007-03-26
![]() in a possibly high d-dimensional
space into a space spanned by the eigenvectors of the covariance matrix
in a possibly high d-dimensional
space into a space spanned by the eigenvectors of the covariance matrix
![]() of the data points. In the new space the different dimensions
(the principal components) of the data points are totally de-correlated and
the energy contained in the data, in terms of the sum of the variances in
all dimensions, is optimally compacked into a small number of components,
so that a large number of components can be discarded without losing much
information in the data, i.e., the dimensionality of the space can be much
reduced.
of the data points. In the new space the different dimensions
(the principal components) of the data points are totally de-correlated and
the energy contained in the data, in terms of the sum of the variances in
all dimensions, is optimally compacked into a small number of components,
so that a large number of components can be discarded without losing much
information in the data, i.e., the dimensionality of the space can be much
reduced.