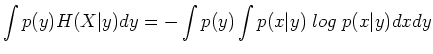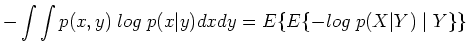Next: Mutual information
Up: Appendix
Previous: Appendix
The entropy of a distribution 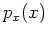 is defined as
is defined as
Entropy represents the uncertainty of the random variable. Among all
distributions, uniform distribution has maximum entropy over a finite
region ![$[a,b]$](img159.png) , while Gaussian distribution has maximum entropy over
the entire real axis.
, while Gaussian distribution has maximum entropy over
the entire real axis.
The joint entropy of two random variables 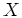 and
and 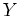 is defined as
is defined as
The conditional entropy of 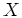 given
given 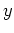 is
is
and the conditional entropy of 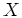 given
given 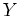 is
is
Ruye Wang
2018-03-26
![]() is defined as
is defined as
![]() and
and ![]() is defined as
is defined as
![]() given
given ![]() is
is