


Next: Appendix
Up: ica
Previous: Preprocessing for ICA
Summarizing the objective functions discussed above, we see a common goal of
maximizing a function
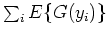 , where
, where
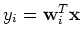 is a component of
is a component of
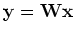
where
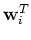 is the ith row vector in matrix
is the ith row vector in matrix 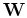 . We first
consider one particular component (with the subscript i dropped). This is an
optimization problem which can be solved by Lagrange multiplier method with
the objective function
. We first
consider one particular component (with the subscript i dropped). This is an
optimization problem which can be solved by Lagrange multiplier method with
the objective function
The second term is the constraint representing the fact that the rows and
columns of the orthogonal matrix 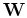 are normalized, i.e.,
are normalized, i.e.,
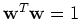 . We set the derivative of
. We set the derivative of
 with
respect to
with
respect to 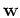 to zero and get
to zero and get
where 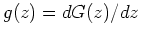 is the derivative of function
is the derivative of function 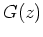 . This algebraic
equation system can be solved iteratively by Newton-Raphson method:
. This algebraic
equation system can be solved iteratively by Newton-Raphson method:
where
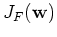 is the Jacobian of function
is the Jacobian of function
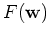 :
:
The first term on the right can be approximated as
and the Jacobian becomes diagonal
and the Newton-Raphson iteration becomes:
Multiplying both sides by the scaler
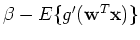 ,
we get
,
we get
Note that we still use the same representation 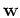 for the
left-hand side, while its value is actually multiplied by a scaler. This is
taken care of by renormalization, as shown in the following FastICA algorithm:
for the
left-hand side, while its value is actually multiplied by a scaler. This is
taken care of by renormalization, as shown in the following FastICA algorithm:
- Choose an initial random guess for
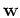
- Iterate:
- Normalize:
- If not converged, go back to step 2.
This is a demo
of the FastICA algorithm.



Next: Appendix
Up: ica
Previous: Preprocessing for ICA
Ruye Wang
2018-03-26
![]() , where
, where
![]() is a component of
is a component of
![]()
![\begin{displaymath}{\mathbf w} \Leftarrow {\mathbf w}-\frac{1}{E\{g'({\mathbf w}...
...mathbf x}g( {\mathbf w}^T {\mathbf x} ) \}-\beta {\mathbf w}]
\end{displaymath}](img153.png)