Formulation of the Problem

A typical example is the ``cocktail party problem''. (See a demo.) Given the signals $x_j(t)$ from $m$ microphones recording $n$ speakers in the room ($m\ge n$), one wants to recover the voice $s_i(t)$ of each speaker. The problem can be formulated as

• Given
  
  $$x_i(t)=\sum_{j=1}^n a_{ij} s_j(t)\;\;\;\;\;(i=1,\cdots,m)$$
  
  
  or in matrix form
  
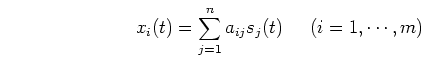
  $$\left[ \begin{array}{c} x_1 \cdots x_m \end{array} \rig... ...} \right] \;\;\;\;\;\;\;\mbox{or}\;\;\;\;\;\;\; {\mathbf x=As}$$
  
  

• Find
  • the estimation ${\mathbf y=Wx}$ of the source variables $s_j(t)$ the independent components,
  • and the linear combination matrix ${\mathbf A}$.

This is a blind source separation (BSS) problem, i.e., to separate linearly mixed source signals. The word ``blind'' means that we do not assume any prior knowledge about sources ${\mathbf s}$ or the mixing process ${\mathbf A}$ except that the source signals $s_i$ are statistically independent.

Although this BSS problem seems severely under constrained, the independent component analysis (ICA) can find nearly unique solutions satisfying certain properties.

ICA can be compared with principal component analysis (PCA) for decorrelation. Given a set of variables ${\mathbf x}$, PCA finds a matrix ${\mathbf W}$ so that the components of ${\mathbf y=Wx}$ are uncorrelated. Only under the special case when ${\mathbf y}=[y_1,\cdots,y_n]$ are gaussian, are they also independent. In comparison, ICA is a more powerful method in the senese that it satisfies a stronger requirement of finding ${\mathbf W}$ so that the components of ${\mathbf y=Wx}$ are independent (and therefore are also necessarily uncorrelated).