The Gradient Operator

The Gradient (also called the Hamilton operator) is a vector operator for any N-dimensional scalar function $f(x_1,\cdots, x_N)=f({\bf x})$, where ${\bf x}=[x_1,\cdots,x_N]^T$ is an N-D vector variable. For example, when $N=3$, $f({\bf x})$ may represent temperature, concentration, or pressure in the 3-D space. The gradient of this N-D function is a vector composed of $N$ components for the $N$ partial derivatives:

$${\bf g}({\bf x})=\bigtriangledown f({\bf x})=\frac{d}{d{\bf x}}f(... ...bf x})}{\partial x_1},\cdots, \frac{\partial f({\bf x})}{\partial x_N}\right]^T$$ (10)

• The direction $\angle {\bf g}$ of the gradient vector ${\bf g}$ is the direction in the N-D space along which the function $f({\bf x})$ increases most rapidly.
• The magnitude $\vert{\bf g}\vert$ of the gradient ${\bf g}$ is the rate of the increment.

In image processing we only consider 2-D field:

$$\bigtriangledown=\left[\begin{array}{c} \frac{\partial}{\partial x}\\ \\ \frac{\partial}{\partial y} \end{array}\right]$$ (11)

When applied to a 2-D function $f(x,y)$, this operator produces a vector function:

$${\bf g}=\bigtriangledown f(x,y) =\left[ \begin{array}{c}\frac{\pa... ... \end{array} \right] =\left[ \begin{array}{c} f_x \\ \\ f_y \end{array} \right]$$ (12)

where $f_x=\partial f/\partial x$ and $f_y=\partial f/\partial y$. The direction and magnitude of ${\bf g}$ are respectively

$$\angle {\bf g}=\tan^{-1} (f_y/f_x),\;\;\;\;\;\;\;\vert\vert{\bf g}\vert\vert =\sqrt{f_x^2+f_y^2}$$ (13)

Now we show that $f(x,y)$ increases most rapidly along the direction of ${\bf g}=\vec{g}(x,y)$ and the rate of increment is equal to the magnitude of ${\bf g}=\vec{g}(x,y)$.

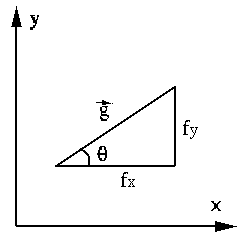
Consider the directional derivative of $f(x,y)$ along an arbitrary direction $r$:

$$\frac{d}{dr}f(x,y)=\frac{\partial f}{\partial x}\frac{dx}{dr}+ \frac{\partial f}{\partial y}\frac{dy}{dr}=f_x \cos\,\theta+f_y\sin\theta$$ (14)

This directional derivative is a function of $\theta$, defined as the angle between directions $r$ and the positive direction of $x$. To find the direction along which $df/dr$ is maximized, we let

$$\frac{d}{d\theta} \frac{df(x,y)}{dr} =\frac{d}{d\theta} (f_x \cos\,\theta+f_y\sin\theta) =-f_x \sin\theta +f_y \cos\,(\theta)=0$$ (15)

Solving this for $\theta$, we get

$$f_x \sin\theta=f_y \cos\,\theta$$ (16)

i.e.,

$$\theta =\tan^{-1} \left(\frac{f_y}{f_x}\right)$$ (17)

which is indeed the direction $\angle {\bf g}$ of ${\bf g}=\vec{g}(x,y)$.

From $\tan\, \theta=f_y/f_x$, we can also get

$$\sin\theta=\frac{f_y}{\sqrt{f_x^2+f_y^2}},\;\;\;\; \cos\,\theta=\frac{f_x}{\sqrt{f_x^2+f_y^2}}$$ (18)

Substituting these into the expression of $df/dr$, we obtain its maximum magnitude,

$$\left. \frac{d}{dr}f(x,y) \right\vert _{max} =\frac{f_x^2+f_y^2}{\sqrt{f_x^2+f_y^2}}=\sqrt{f_x^2+f_y^2}$$ (19)

which is the magnitude of $\vec{g}(x,y)$.