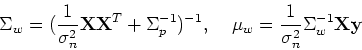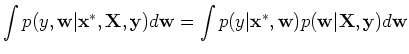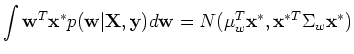Next: Nonlinar Regression
Up: Gaussiaon Process
Previous: Gaussiaon Process
In a general regression problem, the observed data (training data) are
where
![${\bf x}^{(n)}=[x_1^{(n)},\cdots,x_d^{(n)}]^T$](img2.png) is a set of
is a set of  input
vectors of dimensionality of
input
vectors of dimensionality of 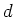 , and
, and 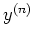 is the corresponding output
scalar assumed to be generated by some underlying processing described by
a function
is the corresponding output
scalar assumed to be generated by some underlying processing described by
a function 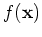 with addititive noise, i.e.,
with addititive noise, i.e.,
The goal of the regression is to infer the function 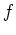 based on
based on 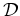 ,
and make prediction of the output
,
and make prediction of the output 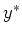 when the input is
when the input is 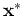 .
.
The simplest form of regression is linear regression based on the assumption
that the underlying function 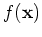 is a linear combination of all
components of the input vector with weights
is a linear combination of all
components of the input vector with weights
![${\bf w}=[w_1,\cdots,w_d]^T$](img12.png) :
:
This can be expressed in matrix form for all 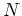 data points:
data points:
where
![${\bf X}=[{\bf x}_1,\cdots,{\bf x}_N]$](img15.png) is an
is an 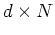 matrix whose
nth column is for the input vector
matrix whose
nth column is for the input vector 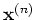 and
and 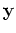 is an
N-dimensional vector for the
is an
N-dimensional vector for the 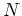 output values. In general,
output values. In general, 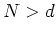 and the
linear regression can be solved by least-squares method to get
and the
linear regression can be solved by least-squares method to get
where
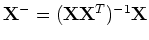 is the psudo inverse of
matrix
is the psudo inverse of
matrix 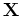 .
.
Alternatively, the regression problem can be viewed as a Bayesian inference
process. We can assume both the model parameters and the noise are normally
distributed:
i.e., the noise 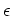 in the
in the 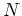 different data points is independent.
The likelihood of the model parameters
different data points is independent.
The likelihood of the model parameters 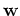 given the data
given the data 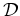 is
is
According to Bayesian theorem, the posterior of the parameters is proportional
to the product of the likelihood and the prior:
where
The predictive distribution of 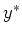 given
given 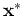 is the average over all
possible parameter values weighted by their posterior probability:
is the average over all
possible parameter values weighted by their posterior probability:



Next: Nonlinar Regression
Up: Gaussiaon Process
Previous: Gaussiaon Process
Ruye Wang
2006-11-14
![]() is a linear combination of all
components of the input vector with weights
is a linear combination of all
components of the input vector with weights
![]() :
:
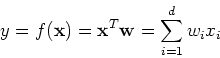
![$\displaystyle \prod_{n=1}^N \frac{1}{\sqrt{2\pi\sigma_n^2}}exp[-\frac{(y^{(n)}-{\bf w}^T{\bf x}^{(n)})^2}{2\sigma_n^2}]=N({\bf X}^T{\bf w},\sigma_n^2 I)$](img29.png)
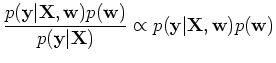
![$\displaystyle c_1\;exp[-\frac{1}{2}(\frac{1}{\sigma_n^2}({\bf y}-{\bf X}^T{\bf w})^T({\bf y}-{\bf X}^T{\bf w})+{\bf w}^T\Sigma_p^{-1} {\bf w})]$](img32.png)
![$\displaystyle c_1\;exp[-\frac{1}{2}(\frac{1}{\sigma_n^2}{\bf y}^T{\bf y}+\frac{...
...}
-\frac{2}{\sigma_n^2}{\bf w}^T{\bf X}{\bf y}+{\bf w}^T\Sigma_p^{-1} {\bf w})]$](img33.png)
![$\displaystyle c_2 \;exp[-\frac{1}{2}({\bf w}^T (\frac{1}{\sigma_n^2}{\bf X}{\bf X}^T+\Sigma_p^{-1}){\bf w}) -\frac{1}{\sigma_n^2}{\bf w}^T{\bf X} {\bf y} ]$](img34.png)
![$\displaystyle c_3 \;exp[-\frac{1}{2}({\bf w}-\mu_w)^T\Sigma_w^{-1}({\bf w}-\mu_w)]=N({\bf w}, \mu_w,\Sigma_w)$](img35.png)