Fourier Descriptor

Let $x[m]$ and $y[m]$ be the coordinates of the mth pixel on the boundary of a given 2D shape containing $N$ pixels, a complex number can be formed as $z[m]=x[m]+jy[m]$, and the Fourier Descriptor (FD) of this shape is defined as the DFT of $z[m]$:

$$Z[k]=DFT[z[m]]=\frac{1}{N}\sum_{m=0}^{N-1}z[m]e^{-j2\pi mk/N}\;\;\;(k=0,\cdots,N-1)$$

FD can be used as a representation of 2D closed shapes independent of its location, scaling, rotation and starting point. For example, we could use $M<N$ FDs corresponding to the low frequency components of the boundary to represent the 2D shape. The reconstructed shape based on these FDs approximate the shape without the details (corresponding to the high frequency components susceptible to noise). However, note that since the Fourier transform is a complex transform, the frequency spectrum has negative frequencies as well as positive frequencies, with the DC component in the middle. Therefore the inverse transform with $M<N$ components needs to contain both positive and negative terms:

$$\hat{z}[m]=\sum_{k=-M/2}^{M/2} Z[k]e^{j2\pi mk/N}\;\;\;(m=0,\cdots,N-1)$$

The following figure shows an image of Gumby:

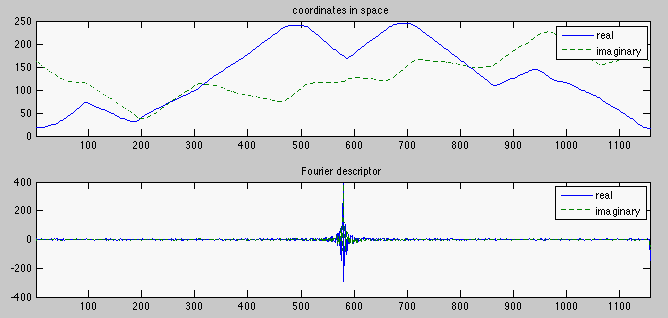
The top part of the following image shows the $x$ (horizontal, red-dashed curve) and $y$ (vertical, blue-continuous curve) coordinates of the $N=1257$ pixels on the boundary of the shape, while the bottom part shows the real and imaginary parts of the frequency components, the Fourier descriptors (FD), of the boundary:

The following image shows the reconstruction of Gumby based on the first $M<N$ low frequency components (excluding the DC). Top: $M=1,\;2,\;3$, and $4$; middle: $M=5,\;6,\;7$, and $8$; bottom: $M=10,\;20,\;30$, and $M=N=1,257$.

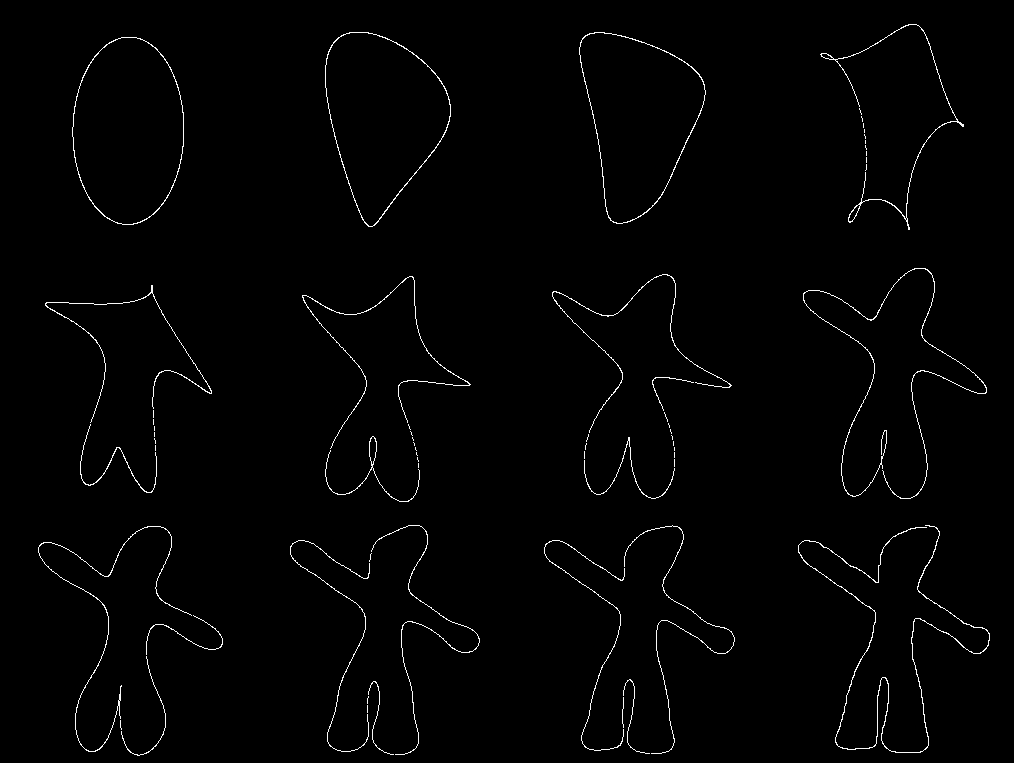
It can be seen that the reconstructed figures using a small percentage of the frequency components are very similar to the actual figure, which can be reconstructed using one hundred percent of the FDs.

Fourier discriptor has the following properties:

• Translation

  If the 2D shape is translated by a distance $z_0=x_0+jy_0$:
  

  $$z'[m]=z[m]+z_0\;\;\;(m=0,\cdots,N-1)$$
  
  
  its FD becomes
  

  $$Z'[k] = \frac{1}{N}\sum_{m=0}^{N-1}[z[m]+z_0]e^{-j2\pi mk/N}$$

  $$= \frac{1}{N}\sum_{m=0}^{N-1}z[m]e^{-j2\pi mk/N}+ \frac{1}{N}\sum_{m=0}^{N-1}z_0e^{-j2\pi mk/N}$$

  $$= Z[k]+z_0 \delta[k]$$

  
  
  i.e., the translation only affects the DC component $Z(0)$ of the FD.

• Scaling

  If the 2D shape is scaled (with respect to origin) by a factor $S$:
  

  $$z'[m]=S\;z[m]$$
  
  
  its FD is scaled by the same factor:
  
  $$Z'[k]=S\;Z[k]$$
  
  

• Rotation

  If the 2D shape is rotated about the origin by an angle $\phi$:
  

  $$z'[m]=z[m]\;e^{j\phi}$$
  
  
  its FD is multiplied by the same factor
  
  $$Z'[k]=Z[k]\;e^{j\phi}$$
  
  

• Starting Point

  If the starting point on the boundary is shifted from 0 to $m_0$:
  

  $$z'[m]=z(m-m_0)$$
  
  
  by time shifting theorem, its FD becomes
  
  $$Z'[k]=Z[k]e^{-j2\pi m_0k/N}$$