Distances

Any distance metric $D(p,q)$ between pixels $p$ and $q$ must satisfy:

1. $D(p,q) \ge 0,\;\; (D(p,q)=0 \;\;$iff$\;\; p=q)$;
2. $D(p,q)=D(q,p)$;
3. $D(p,q) \le D(p,r)+D(r,q)$.

where $r$ is an arbitrary pixel.

Specifically, the distance between pixels $p$ at $(x,y)$ and $q$ at $(u,v)$ can be defined by one of the following:

• Euclidean distance

  $$D_E(p,q)=\sqrt{(x-u)^2+(y-v)^2}=[\vert x-u\vert^2+\vert y-v\vert^2]^{1/2}$$ (11)

• City-block distance

  $$D_4(p,q)=\vert x-u\vert+\vert y-v\vert=[\vert x-u\vert^1+\vert y-v\vert^1]^{1/1}$$ (12)

• Chess-board distance

  $$D_8(p,q)=max\{\vert x-u\vert,\vert y-v\vert\}=[\vert x-u\vert^\infty+\vert y-v\vert^\infty]^{1/\infty}$$ (13)

From these definitions we see that a general distance definition is

$$D(p,q)=[\vert x-u\vert^L+\vert y-v\vert^L]^{1/L}$$ (14)

where $L$ can take any value between 1 and $\infty$. When $L$ is small (e.g., 1), contributions of the two dimensions are treated equally, but when $L$ is large (e.g., toward $\infty$), the dimension with larger contribution is more emphasized. Note that other types of distance metrics can also be used.

The $D_E$ distance in digital image approximates the actual Euclidean distance in continuous situation.

The numbers in the following array show the $D_4$ distances to the pixel in the center. Note that all 4-neighbors have distance 1.

4	3	2	3	4
3	2	1	2	3
2	1	0	1	2
3	2	1	2	3
4	3	2	3	4

The numbers here are the $D_8$ distances to the pixel in the center. Note that all 8-neighbors have distance 1.

2	2	2	2	2
2	1	1	1	2
2	1	0	1	2
2	1	1	1	2
2	2	2	2	2

The following figure shows the iso-distance contours composed of all points having equal distance to the center point. The circle is for Euclidean distance, the square is for the $D_8$ distance, the diamond is for the $D_4$ distance.

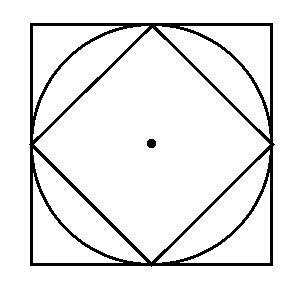
Distance between two connected pixels can be defined as the number of hops from one pixel to the next along the shortest path connecting the two pixels, according to the definition of connectivity (4, 8, or mix-connected).

The upper-right pixel is 8 and mix-connected to the lower-left pixel with a $D_8$ distance 2:

0	0	1
0	1	0
1	0	0

The upper-right pixel is 4 and mix-connected to the lower-left pixel with a $D_4$ distance 4:

0	1	1
0	1	0
1	1	0