next up previous
Next: Inter-pixel Redundancy and Compression Up: Image Compression with Huffman Previous: Shannon's source coding theorem

The algorithm

The Huffman coding is form of entropy coding which implements the coding idea discussed above. If a random number has $N=2^n$ possible outcomes (symbols), it is obvious that these outcomes can be coded by $n$ bits. For example, as the pixels in a digital image can take $2^8=256$ possible gray values, we need $n=8$ bits to represent each pixel and $nM^2$ bits to represent an image of $M \times M$ pixels. By Huffman coding, however, it is possible to use on average fewer than $n=8$ bits to represent each pixel.

In general, Huffman coding encodes a set of $N$ symbols (e.g., $N=256$ gray levels in a digital image) with binary code of variable length, following this procedure:

  1. Estimate the probability $P_i$ for each of the $N$ symbols ( $i=1,2,\cdots,N$);
  2. Sort these $P_i$'s in descending order (top down);
  3. Forward pass (left to right): combine the two smallest $P_i$'s at the bottom and resort their sum with all other probabilities, repeat this step until there are only two probabilities left;
  4. Backward pass (right to left): add a bit (0 or 1) to the binary codes of the two probabilities newly emerging at each step, repeat this step until all the initial $N$ symbols are encoded.
As the result of Huffman coding, all symbols are encoded optimally in the sense that more probable symbols are encoded by shorter binary codes, so that the average length (number of bits) of the codes for these symbols is minimized.

To illustrate how much compression the Huffman coding can achieve and how the compression rate is related to the content of the image, consider the following examples of compressing an image of $N=2^n=2^2=4$ gray levels, each with probability $P_i$ for a pixel to be at the ith gray level ($i=1,2,3,4$) (the histogram of the image).

Example 0: $P_1=1$, $P_2=P_3=P_4=0$, i.e., all pixels take the same value. The image contains 0 bits uncertainty (no surprise) or information and requires 0 bits to transmit.

Example 1:

\begin{displaymath} \begin{tabular}{ll}\hline $P_i$ & code \hline 0.9 & 0 \\ 0.1 & 1 \\ 0.0 & \\ 0.0 & \hline \end{tabular}\end{displaymath}

The uncertainty is

\begin{displaymath}H=-0.9\; log_2\; 0.9-0.1\;log_2\;0.1=0.469 \;\mbox{ bits} \end{displaymath}

Although the uncertainty is less than half of that in the previous case, it still requires one bit to encode the information.

Example 2:

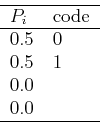
\begin{displaymath} \begin{tabular}{ll}\hline $P_i$ & code \hline 0.5 & 0 \\ 0.5 & 1 \\ 0.0 & \\ 0.0 & \hline \end{tabular}\end{displaymath}

The uncertainty is

\begin{displaymath}H=-0.5\; log_2\; 0.5-0.5\;log_2\;0.5=1.0 \;\mbox{ bits} \end{displaymath}

which requires 1 bit to encode the information.

Example 3:

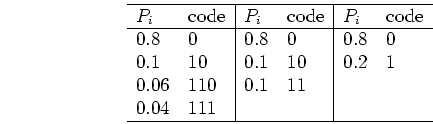
\begin{displaymath} \begin{tabular}{ll\vert ll\vert ll}\hline $P_i$ & code & $... ...0 & 0.1 & 11 & & \\ 0.04 & 111 & & & & \hline \end{tabular}\end{displaymath}

The average number of bits for each pixel is

\begin{displaymath}0.8\times 1 + 0.1\times 2 + 0.06\times 3+0.04\times 3=1.3 \end{displaymath}

and the uncertainty is

\begin{displaymath} H=-0.8\;log_2 0.8-0.1\;log_2 0.1-0.06\;log_2 0.06-0.04\;log_2 0.04=1.019 \;\mbox{ bits} \end{displaymath}

Example 4:

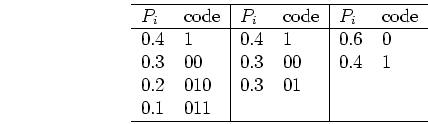
\begin{displaymath} \begin{tabular}{ll\vert ll\vert ll}\hline $P_i$ & code & $... ...10 & 0.3 & 01 & & \\ 0.1 & 011 & & & & \hline \end{tabular}\end{displaymath}

The average number of bits for each pixel is

\begin{displaymath}0.4\times 1 + 0.3\times 2 + 0.2\times 3+0.1\times 3=1.9 \;\mbox{ bits} \end{displaymath}

and the uncertainty is

\begin{displaymath} H=-0.4\;log_2 0.4-0.3\;log_2 0.3-0.2\;log_2 0.2-0.1\;log_2 0.1=1.846 \;\mbox{ bits} \end{displaymath}

Example 5:

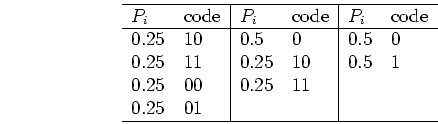
\begin{displaymath} \begin{tabular}{ll\vert ll\vert ll}\hline $P_i$ & code & $... ...0 & 0.25 & 11 & & \\ 0.25 & 01 & & & & \hline \end{tabular}\end{displaymath}

The average number of bits for each pixel is

\begin{displaymath}0.25\times 2 + 0.25\times 2 + 0.25\times 2+0.25\times 2=2 \;\mbox{ bits} \end{displaymath}

and the uncertainty is

\begin{displaymath} H=-0.25\;log_2 0.25-0.25\;log_2 0.25-0.25\;log_2 0.25-0.25\;log_2 0.25=2 \;\mbox{ bits} \end{displaymath}

This image has the maximum information (uncertainty) and therefore requires $n=log_2 4=2$ bits to encode each of its pixels.

From these examples it can be seen that with variable-length coding the average number of bits needed to encode a pixel may be reduced from $n=log_2 N$. The amount of reduction, or the compression rate, depends on the amount of uncertainty or information contained in the image. If the image has only a single gray level, it contains 0 bits information and requires 0 bits to encode; but if the image has $N=2^n$ equally likely gray levels, it contains maximum amount of $n$ bits information requiring $n$ bits to encode.

next up previous
Next: Inter-pixel Redundancy and Compression Up: Image Compression with Huffman Previous: Shannon's source coding theorem
Ruye Wang 2021-03-28