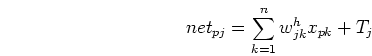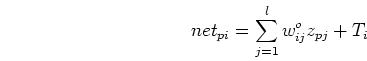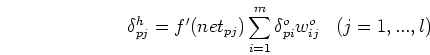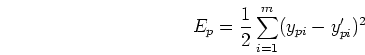Next: The Structure and Purpose
Up: bp
Previous: The Gradient Descent Method
Every time a particular pattern pair 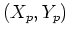 is presented at the input
layer, all the weights are modified in the following manner.
is presented at the input
layer, all the weights are modified in the following manner.
- Define error energy
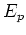 at the output layer:
at the output layer:
where
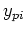 is the desired output, and
is the desired output, and 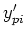 is the actual output
is the actual output
- Find gradient of
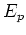 in output weight space
in output weight space
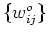 :
:
- Update
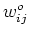 to minimize
to minimize 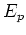 with gradient descent method:
with gradient descent method:
where
and 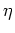 is the learning rate.
is the learning rate.
- Relate
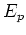 to the hidden layer weights
to the hidden layer weights 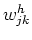
- Find gradient of
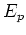 in hidden weight space
in hidden weight space
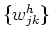 :
:
where
- Update
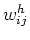 to minimize
to minimize 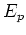 with gradient descent method
with gradient descent method
where
Summary of Back Propagation Training
The following is for one training pattern pair 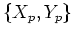 .
.
- Apply
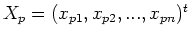 to the input nodes;
to the input nodes;
- Compute net input to hidden nodes
- Compute output from hidden nodes
- Compute net input to output nodes
- Compute output from output nodes
- Find error terms for all output nodes (not quite the same as defined
previously)
where
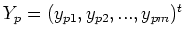 is the desired output for
is the desired output for
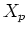 .
.
- Find error terms for all hidden nodes (not quite the same as defined
previously)
- Update weights to output nodes
- Update weights to hidden nodes
- Compute
When this error is acceptably small for all of the training pattern pairs,
training can be discontinued.
Competitive learning Network



Next: The Structure and Purpose
Up: bp
Previous: The Gradient Descent Method
Ruye Wang
2002-12-09
![]() is presented at the input
layer, all the weights are modified in the following manner.
is presented at the input
layer, all the weights are modified in the following manner.
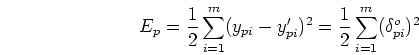
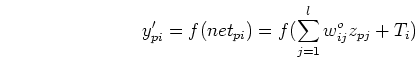
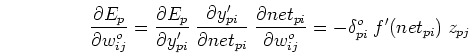
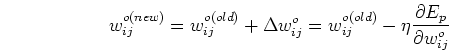

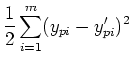
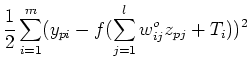
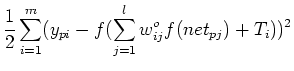
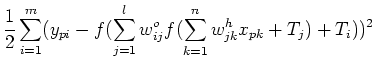
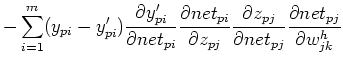
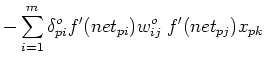
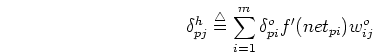
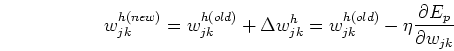
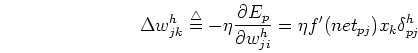
![]() .
.