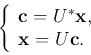Definition: A vector space is a set ![]() with two operations of
addition and scalar multiplication defined for its members, referred to
as vectors.
with two operations of
addition and scalar multiplication defined for its members, referred to
as vectors.
Definition:
An inner product on a vector space ![]() is a function that maps two vectors
is a function that maps two vectors
![]() to a scalar
to a scalar
![]() and satisfies the following conditions:
and satisfies the following conditions:
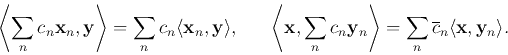
Definition: A vector space with inner product defined is called an inner product space.
Definition: When the inner product is defined, ![]() is called
a unitary space and
is called
a unitary space and ![]() is called a Euclidean space.
is called a Euclidean space.
Examples
![${\bf x}=[\cdots,x[n],\cdots]^\textrm{T}$](img32.png) and
and
![${\bf y}=[\cdots,y[n],\cdots]^\textrm{T}$](img33.png) is defined as
is defined as
![\begin{displaymath}
\langle {\bf x}, {\bf y}\rangle={\bf x}^\textrm{T}\overline...
...] \overline{x}[n]}
=\overline{\langle{\bf y},{\bf x}\rangle}
\end{displaymath}](img34.png)
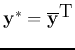 is the conjugate transpose of
is the conjugate transpose of ![\begin{displaymath}
{\bf d}=[\cdots \cdots,1,\cdots \cdots]^T, \;\;\;\;\mbox{i....
...]=\left\{ \begin{array}{ll}1&n=0 0&n\ne 0\end{array}\right.
\end{displaymath}](img37.png)
![\begin{displaymath}\langle {\bf x}, {\bf y}\rangle=\sum_{m=1}^M\sum_{n=1}^N x[m,n]\overline{y}[m,n].\end{displaymath}](img41.png)
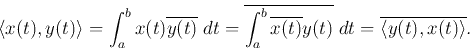
The concept of inner product is of essential importance based on which a whole set of other important concepts can be defined.
Definition:
If the inner product of two vectors ![]() and
and ![]() is zero,
is zero,
![]() , they are orthogonal (perpendicular) to
each other, denoted by
, they are orthogonal (perpendicular) to
each other, denoted by
![]() .
.
Definition:
The norm (or length) of a vector ![]() is defined as
is defined as
The norm ![]() is non-negative and it is zero if and only if
is non-negative and it is zero if and only if
![]() . In particular, if
. In particular, if ![]() , then it is said
to be normalized and becomes a unit vector. Any vector can
be normalized when divided by its own norm:
, then it is said
to be normalized and becomes a unit vector. Any vector can
be normalized when divided by its own norm:
![]() . The
vector norm squared
. The
vector norm squared
![]() can be
considered as the energy of the vector.
can be
considered as the energy of the vector.
Example: In an ![]() -D unitary space, the p-norm of a vector
-D unitary space, the p-norm of a vector
![${\bf x}=[x[1],\ldots,x[N]]^\textrm{T} \in \mathbb{C}^N$](img62.png) is
is
![\begin{displaymath}\vert\vert{\bf x}\vert\vert _p=\left[\sum_{n=1}^N \vert x[n]\vert^p\right]^{1/p}. \end{displaymath}](img63.png)
![\begin{displaymath}\vert\vert{\bf x}\vert\vert _1=\sum_{n=1}^N \vert x[n]\vert \end{displaymath}](img65.png)
![\begin{displaymath}\vert\vert{\bf x}\vert\vert=\sqrt{\langle {\bf x},{\bf x}\ran...
...ght]^{1/2}
=\left[\sum_{n=1}^N \vert x[n]\vert^2\right]^{1/2}. \end{displaymath}](img67.png)
![\begin{displaymath}{\cal E}=\vert\vert{\bf x}\vert\vert^2=\langle {\bf x},{\bf x}\rangle=\sum_{n=1}^N \vert x[n]\vert^2. \end{displaymath}](img68.png)
The concept of ![]() -D unitary (or Euclidean) space can be generalized to an
infinite-dimensional space, in which case the range of the summation will
cover all real integers
-D unitary (or Euclidean) space can be generalized to an
infinite-dimensional space, in which case the range of the summation will
cover all real integers ![]() in the entire real axis
in the entire real axis
![]() .
This norm exists only if the summation converges to a finite value; i.e., the
vector
.
This norm exists only if the summation converges to a finite value; i.e., the
vector ![]() is an energy signal with finite energy:
is an energy signal with finite energy:
![\begin{displaymath}\sum_{n=-\infty}^\infty \vert x[n]\vert^2 < \infty. \end{displaymath}](img73.png)
Similarly, in a function space, the norm of a function vector ![]() is defined as
is defined as
![\begin{displaymath}\vert\vert{\bf x}\vert\vert=\left[ \int_a^b x(t)\overline{x(t...
...{1/2}
=\left[ \int_a^b \vert x(t)\vert^2\; \;dt \right]^{1/2}, \end{displaymath}](img76.png)
Definition:
In a unitary space ![]() , the p-norm distance between two
vectors
, the p-norm distance between two
vectors ![]() and
and ![]() is defined as the p-norm of the difference
is defined as the p-norm of the difference
![]() :
:
![\begin{displaymath}d_p({\bf x},{\bf y})=\left( \sum_{n=1}^N \vert x[n]-y[n]\vert^p\right)^{1/p}. \end{displaymath}](img83.png)
![\begin{displaymath}d_1({\bf x},{\bf y})&=&\sum_{n=1}^N \vert x[n]-y[n]\vert \end{displaymath}](img84.png)
![\begin{displaymath}d({\bf x},{\bf y})=\vert\vert{\bf x}-{\bf y}\vert\vert=\left(\sum_{n=1}^N \vert x[n]-y[n]\vert^2\right)^{1/2}. \end{displaymath}](img85.png)
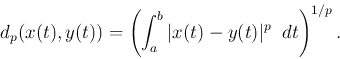
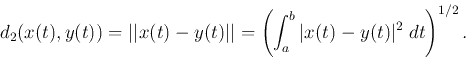
Definition:
A vector space V of all linear combinations of a set of vectors
![]() is called the linear span of the vectors:
is called the linear span of the vectors:
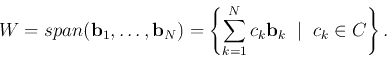
Definition: A set of linearly independent vectors that spans a vector space is called a basis of the space. It these vectors are unitary/orthogonal and normalized, they form an orthonormal basis.
Any vector
![]() can be uniquely expressed as a linear
combination of some
can be uniquely expressed as a linear
combination of some ![]() basis vectors
basis vectors ![]() :
:
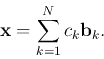
Theorem:
Let ![]() and
and ![]() be any two vectors in a vector space
be any two vectors in a vector space ![]() spanned
by a set of complete orthonormal (orthogonal and normalized) basis vectors
spanned
by a set of complete orthonormal (orthogonal and normalized) basis vectors
![]() satisfying
satisfying
![\begin{displaymath}\langle {\bf x},{\bf u}_l\rangle=\left\langle \sum_k c_k {\bf...
...\langle {\bf u}_k,{\bf u}_l\rangle=\sum_k c_k \delta[k-l]=c_l.
\end{displaymath}](img103.png)
Example: Space ![]() can be spanned by
can be spanned by ![]() orthonormal
vectors
orthonormal
vectors
![]() , where the
, where the ![]() th basis vector is
th basis vector is
![${\bf u}_k=[u[1,k],\ldots,u[N,k]]^\textrm{T}$](img109.png) , that satisfy:
, that satisfy:
![\begin{displaymath}\langle {\bf u}_k,{\bf u}_l\rangle={\bf u}_k^\textrm{T} \over...
...{\bf u}}_l
=\sum_{n=1}^N u[n,k]\overline{u}[n,l]=\delta[k-l]. \end{displaymath}](img110.png)
Any vector
![${\bf x}=[x[1],\ldots,x[N]]^\textrm{T} \in \mathbb{C}^N$](img62.png) can be expressed as
can be expressed as
![\begin{displaymath}{\bf x}=\sum_{k=1}^N c_k {\bf u}_k=[{\bf u}_1,\ldots,{\bf u}_...
...y}{c}c[1] \vdots c[N]\end{array}\right]
={\bf U}{\bf c},
\end{displaymath}](img111.png)
![${\bf c}=[c[1],\ldots,c[N]]^\textrm{T}$](img112.png) and
and
![\begin{displaymath}{\bf U}=[{\bf u}_1,\ldots,{\bf u}_N]=\left[ \begin{array}{ccc...
...ts & \vdots \\
u[N,1] & \ldots & u[N,N] \end{array} \right].
\end{displaymath}](img113.png)
This two equations can be rewritten as a pair of transforms:
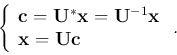
The second equation in the transform pair can also be written in component form as
![\begin{displaymath}x[n]=\sum_{k=1}^N c_k u[k,n],\;\;\;\;\;\;\;\;\;n=1,\ldots,N. \end{displaymath}](img121.png)
Example: In ![]() space composed of all square-integrable
functions defined over
space composed of all square-integrable
functions defined over ![]() , spanned by a set of orthonormal basis
functions
, spanned by a set of orthonormal basis
functions ![]() satisfying:
satisfying:
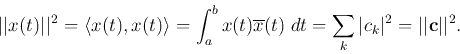
The Fourier transforms
Consider the following four Fourier bases that span four different types of vector spaces for signals that are either continuous or discrete, of finite or infinite duration.
![${\bf u}_k=[e^{j2\pi k0/N},\ldots,e^{j2\pi k(N-1)/N}]^\textrm{T}/\sqrt{N}$](img135.png) (
(
![\begin{displaymath}\langle {\bf u}_k,{\bf u}_l\rangle=\frac{1}{N}\sum_{n=0}^{N-1} e^{j2\pi (k-l)n/N}=\delta[k-l]. \end{displaymath}](img137.png)
![${\bf x}=[x[0],\ldots,x[N-1] ]^\textrm{T}$](img138.png) in
in ![\begin{displaymath}{\bf x}=\sum_{k=0}^{N-1} X[k]{\bf u}_k
=\sum_{k=0}^{N-1} \langle {\bf x},{\bf u}_k\rangle {\bf u}_k, \end{displaymath}](img139.png)
![\begin{displaymath}
x[n]=\frac{1}{\sqrt{N}}\sum_{k=0}^{N-1} X[k] e^{j2\pi kn/N}\;\;\;\;\;\;\;0\le n\le N-1,
\end{displaymath}](img140.png)
![\begin{displaymath}X[k]=\langle {\bf x},{\bf u}_k\rangle=\sum_{n=0}^{N-1} x[n]\o...
...k]
=\frac{1}{\sqrt{N}} \sum_{n=0}^{N-1} x[n] e^{-j2\pi nk/N}. \end{displaymath}](img142.png)
![${\bf u}(f)=[\ldots,e^{j2\pi mf/F},\ldots]^\textrm{T}/\sqrt{F}$](img143.png) (
(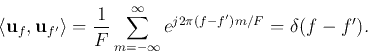
Any vector
![${\bf x}=[\ldots,x[n],\ldots]^\textrm{T}$](img147.png) in this space can be expressed as
in this space can be expressed as
![\begin{displaymath}X(f)=\langle {\bf x},{\bf u}(f)\rangle=\frac{1}{\sqrt{F}}\sum_{n=-\infty}^\infty x[n]e^{-j2\pi f n/F}. \end{displaymath}](img152.png)
![\begin{displaymath}
\langle u_k(t),u_l(t)\rangle=\frac{1}{T}\int_0^\textrm{T} e^{j2\pi (k-l)t/T} \;dt=\delta[k-l].
\end{displaymath}](img156.png)
![\begin{displaymath}
x_T(t)=\sum_{k=-\infty}^\infty X[k]u_k(t)
=\frac{1}{\sqrt{T}}\sum_{k=-\infty}^\infty X[k]e^{j2\pi kt/T},
\end{displaymath}](img158.png)
Definition:
A linear transformation
![]() is a unitary transformation
if it conserves inner products:
is a unitary transformation
if it conserves inner products:
A unitary transformation also conserves any measurement based on the
inner product, such as the norm of a vector, the distance and angle
between two vectors, and the projection of one vector on another. Also,
if in particular
![]() , we have
, we have
Definition
A matrix ![]() is unitary if it conserves inner products:
is unitary if it conserves inner products:
Theorem:
A matrix ![]() is unitary if and only if
is unitary if and only if
![]() ; i.e.,
the following two statements are equivalent:
; i.e.,
the following two statements are equivalent:
A unitary matrix ![]() has the following properties:
has the following properties:
The identity matrix
![]() is a special
orthogonal matrix as its columns (or rows) are orthonormal:
is a special
orthogonal matrix as its columns (or rows) are orthonormal:
![${\bf x}=[x[1],\ldots,x[N]]^\textrm{T} \in \mathbb{C}^N$](img62.png) can be represented
by the standard basis as
can be represented
by the standard basis as
![\begin{displaymath}{\bf x}=\left[\begin{array}{c}x[1] \vdots x[N]\end{array}...
...ray}{c}x[1] \vdots x[N]\end{array}\right]
={\bf I}{\bf x}
\end{displaymath}](img191.png)
![\begin{displaymath}{\bf x}={\bf I}{\bf x}={\bf U} {\bf U}^*{\bf x}={\bf U} {\bf ...
...\vdots c[N]\end{array}\right]
=\sum_{k=1}^N c[k] {\bf u}_k,
\end{displaymath}](img192.png)
![\begin{displaymath}{\bf c}=\left[\begin{array}{c}c[1] \vdots c[N]\end{array}...
...;\;
c[k]={\bf u}_k^*{\bf x}=\langle {\bf x},{\bf u}_k\rangle.
\end{displaymath}](img193.png)
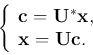
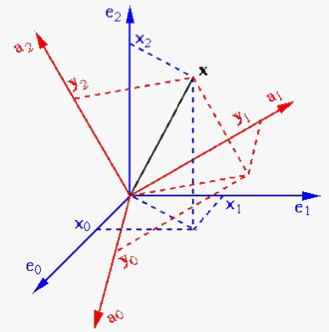
This result can be extended to the continuous transformation for signal vectors
in the form of continuous functions. In general, corresponding to any given
unitary transformation ![]() , a signal vector
, a signal vector ![]() can be alternatively
represented by a coefficient vector
can be alternatively
represented by a coefficient vector
![]() (where
(where ![]() can be
either a set of discrete coefficients
can be
either a set of discrete coefficients ![]() or a continuous function
or a continuous function ![]() ).
The original signal vector
).
The original signal vector ![]() can always be reconstructed from
can always be reconstructed from ![]() by applying
by applying ![]() on both sides of
on both sides of
![]() to get
to get
![]() ; i.e., we get a unitary transform pair in
the most general form:
; i.e., we get a unitary transform pair in
the most general form: