Next: QR Decomposition Up: ch1 Previous: The Power Methods for
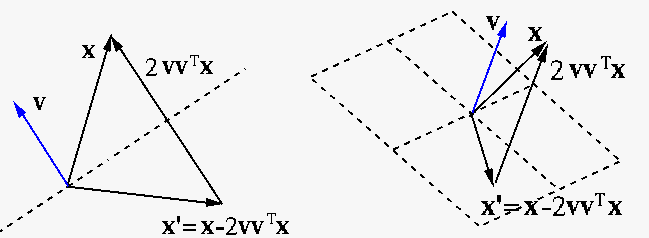
A Householder transformation of a vector 


 is the
projection
of
is the
projection
of  onto the unit vector
onto the unit vector  , and
, and
 is the Householder matrix
that converts
is the Householder matrix
that converts  to its reflection
to its reflection  . Given the
desired reflection
. Given the
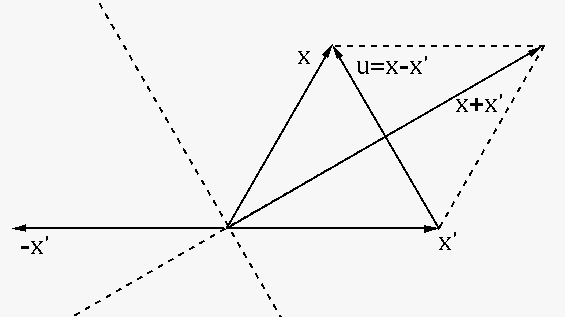
desired reflection  , we can get the normal direction
of the reflection plane
, we can get the normal direction
of the reflection plane
 , and then
normalize it to get
, and then
normalize it to get
 . Although the
Householder transformation is expressed as a linear transformation
. Although the
Householder transformation is expressed as a linear transformation
 , its computational complexity is
, its computational complexity is  , instead
of
, instead
of  for a general matrix multiplication
for a general matrix multiplication  .
.
The Householder matrix 
 |
(52) |
 |
 |
 |
|
 |
 |
(53) |
 . As vector norm is preserved by an
orthogonal transform, we have
. As vector norm is preserved by an
orthogonal transform, we have
 .
.
We can verify that 





 |
 |
 |
|
 |
 |
(54) |
The Householder transformation is typically used to convert a given
vector
![${\bf x}=[x_1,\cdots,x_N]^T$](img245.svg)
![$\displaystyle {\bf x}'=[x'_1,0,\cdots,0]^T=\vert\vert{\bf x}\vert\vert{\bf e}_1$](img246.svg) |
(55) |
![${\bf e}_1=[1,0,\cdots,0]^T$](img247.svg) is the first standard basis vector.
In this case, the normal vector needs to be:
is the first standard basis vector.
In this case, the normal vector needs to be:
 |
(56) |
![${\bf x}'=\vert\vert{\bf x}\vert\vert\;[1,0,\cdots,0]^T$](img249.svg) is always a real vector. However, when the given vector
is always a real vector. However, when the given vector  is complex, the reflection needs to be kept complex as well, instead
of being forced to be real. In this case, we should use
is complex, the reflection needs to be kept complex as well, instead
of being forced to be real. In this case, we should use
![${\bf x}'=\vert\vert{\bf x}\vert\vert\;[x_1/\vert x_1\vert,0,\cdots,0]^T$](img250.svg) , where
, where  is a normalized complex value based on the first entry of the given
vector
is a normalized complex value based on the first entry of the given
vector  .
.
By applying a sequence of Householder transformations to the rows
and columns of a given square matrix 





We first consider converting a symmetric matrix


![$\displaystyle {\bf Q}_1=\left[\begin{array}{c\vert ccc}
1&0&\cdots&0\\ \hline 0& & & \\ \vdots & &{\bf P}_{N-1} & \\
0& & & \end{array}\right]$](img253.svg) |
(57) |
 is an
is an  dimensional Householder matrix that
converts
dimensional Householder matrix that
converts
![$[a_{21},\cdots,a_{N1}]^T$](img256.svg) containing the last
containing the last  elements of
the first column of
elements of
the first column of  into
into
![$[a'_{21},0,\cdots,0]^T$](img257.svg) . Note that
. Note that
 is also symmetric and orthogonal.
Pre-multiplying
is also symmetric and orthogonal.
Pre-multiplying  to
to  we get:
we get:
 |
 |
![$\displaystyle \left[\begin{array}{c\vert ccc}
1&0&\cdots&0\\ \hline 0& & & \\ \...
...ine
a_{21}& & & \\ \vdots & &{\bf A}_{N-1} & \\ a_{N1} & & & \end{array}\right]$](img261.svg) |
|
 |
![$\displaystyle \left[\begin{array}{c\vert ccc}a_{11}&a_{12}&\cdots&a_{1N}\\ \hli...
...\\ a_{N1}\end{array}\right)
& & {\bf P}_{N-1}{\bf A}_{N-1} & \end{array}\right]$](img262.svg) |
||
 |
![$\displaystyle \left[\begin{array}{c\vert ccc}a_{11}&a_{12}&\cdots&a_{1N}\\ \hli...
...0 & & & \\ \vdots & &{\bf P}_{N-1}{\bf A}_{N-1} &
\\ 0 & & & \end{array}\right]$](img263.svg) |
(58) |
 is an
is an  dimensional submatrix containing
the lower-right
dimensional submatrix containing
the lower-right  by
by  elements of
elements of  . We see that
the last
. We see that
the last  components of the first column of the resulting matrix
components of the first column of the resulting matrix
 are zero. We next post-multiply
are zero. We next post-multiply  to
modify the first row:
to
modify the first row:
 |
 |
![\begin{displaymath}\left[\begin{array}{c\vert ccc}
a_{11}&a_{12}&\cdots&a_{1N}\\...
...{\bf P}_{N-1}&\\
\vdots & & & \\ 0& & & \\
\end{array}\right]\end{displaymath}](img268.svg) |
|
 |
![$\displaystyle \left[\begin{array}{c\vert ccc}a_{11}& &
[a_{12},\cdots,a_{1N}]{\...
...dots & &{\bf P}_{N-1}{\bf A}_{N-1}{\bf P}_{N-1} &
\\ 0 & & & \end{array}\right]$](img269.svg) |
||
 |
![$\displaystyle \left[\begin{array}{c\vert cccc}a_{11}&a'_{12}&0&\cdots&0\\ \hlin...
...ts &&&{\bf P}_{N-1}{\bf A}_{N-1}{\bf P}_{N-1} &
\\ 0 & & & & \end{array}\right]$](img270.svg) |
(59) |
 components of the first row and column
of
components of the first row and column
of  become zero.
become zero.
This process is then repeated for the lower-right submatrix



![$\displaystyle {\bf Q}_2=\left[\begin{array}{cc\vert ccc}
1&0&0&\cdots&0\\ 0&1&0...
...ne
0&0& & & \\ \vdots &\vdots& &{\bf P}_{N-2} & \\
0&0& & & \end{array}\right]$](img272.svg) |
(60) |
![$\displaystyle {\bf A}''={\bf Q}_2{\bf A}'{\bf Q}_2={\bf Q}_2{\bf Q}_1{\bf A}{\b...
...{\bf P}_{N-2}{\bf A}_{N-2}{\bf P}_{N-2}& \\
0 &0& & & & \\
\end{array}\right]$](img273.svg) |
(61) |
 components of the second row and column
of
components of the second row and column
of  become zero. This process is repeated until after
become zero. This process is repeated until after
 iterations the N-D matrix
iterations the N-D matrix  is converted into a
tridiagonal matrix, with all entries
is converted into a
tridiagonal matrix, with all entries  equal to zero except
those along the sub-diagonal (
equal to zero except
those along the sub-diagonal ( ), the superdiagonal (
), the superdiagonal ( )
as well as the main diagonal (
)
as well as the main diagonal ( ):
):
 |
(62) |
 . Note
that
. Note
that  is not symmetric (a product of symmetric matrices is
not symmetric), but it is orthogonal:
is not symmetric (a product of symmetric matrices is
not symmetric), but it is orthogonal:
 |
 |
 |
|
 |
 |
(63) |
 , a similarity transformation
of
, a similarity transformation
of  , has the same eigenvalues as
, has the same eigenvalues as  .
.
Based on the example tridiagonalization above, we make a few notes
 .
However, as its rows are not the same as its columns, while the
pre-multiplication of the Householder matrices can convert all entries
below the sub-diagonal to zero, the post-multiplication by the the same
matrices can no longer convert all entries above the super-diagonal to
zero. The resulting matrix
.
However, as its rows are not the same as its columns, while the
pre-multiplication of the Householder matrices can convert all entries
below the sub-diagonal to zero, the post-multiplication by the the same
matrices can no longer convert all entries above the super-diagonal to
zero. The resulting matrix
 , called
Hessenberg matrix, is not tridiagonal, as the entries above the
super-diagonal are non-zero. The non-symmetric matrix could still be
tridiagonalized by post-multiplying the Householder matrices based on
its rows (instead its columns). However, as the post-multiplying matrix
is not the same as pre-multiplying matrix, this is not a similarity
transformation, and the eigenvalues are not preserved.
, called
Hessenberg matrix, is not tridiagonal, as the entries above the
super-diagonal are non-zero. The non-symmetric matrix could still be
tridiagonalized by post-multiplying the Householder matrices based on
its rows (instead its columns). However, as the post-multiplying matrix
is not the same as pre-multiplying matrix, this is not a similarity
transformation, and the eigenvalues are not preserved.
 into a upper
triangular matrix
into a upper
triangular matrix  by a sequence of Householder transformations
applied only to the columns of
by a sequence of Householder transformations
applied only to the columns of  . This is the QR decomposition
to be considered in the next section. Note that this is not a similarity
transformation,
. This is the QR decomposition
to be considered in the next section. Note that this is not a similarity
transformation,  and
and  do not have the same eigenvalues.
However, it can be used as an iterative step in an algorithm for solving
the eigenvalue problem.
do not have the same eigenvalues.
However, it can be used as an iterative step in an algorithm for solving
the eigenvalue problem.
 into a lower of
upper triangular matrix, or even a diagonal matrix. However, this is
not a similarity transformation, and the eigenvalues are not preserved.
While this method can be used to find the inverse of
into a lower of
upper triangular matrix, or even a diagonal matrix. However, this is
not a similarity transformation, and the eigenvalues are not preserved.
While this method can be used to find the inverse of  , it
cannot be used for solving eigenvalue problem.
, it
cannot be used for solving eigenvalue problem.
Examples: Consider two matrices, one symmetric, one non-symmetric:
![$\displaystyle {\bf A}=\left[\begin{array}{rrrr}
3 & 1 & -4 & 2\\ 1 & 4 & 3 & -1\\
-4 & 3 & -2 & 3\\ 2 & -1 & 3 & 2\end{array}\right]
$](img288.svg)
![$\displaystyle {\bf Q}=\left[\begin{array}{rrrr}
1 & 0 & 0 & 0 \\
0 & -0.218 ...
... 0 & -0.973 & -0.230 & 0.026\\
0 & -0.078 & 0.430 & 0.899\end{array}\right]
$](img289.svg)
![$\displaystyle {\bf QAQ}^T=\left[\begin{array}{rrrr}
3.000 & -4.583 & 0 & 0 \\ ...
...\\
0 & -1.218 & 5.039 & -0.364\\
0 & 0 & -0.364 & 3.532\end{array}\right]
$](img290.svg)
 and the symmetric matrix
and the symmetric matrix  share the same eigenvalues
share the same eigenvalues
 .
.
 can be converted into
a Hessenberg matrix
can be converted into
a Hessenberg matrix
![$\displaystyle {\bf A}=\left[\begin{array}{rrrr}
3 & 1 & -4 & 2 \\ -2 & 4 & 3 & -1\\
1 & 2 & -2 & 3 \\ 1 & -1 & 4 & 2\end{array}\right]
$](img293.svg)
![$\displaystyle {\bf Q}=\left[\begin{array}{rrrr}
1 & 0 & 0 & 0 \\
0 & -0.817 ...
...
0 & -0.043 & -0.748 & 0.662\\
0 & 0.576 & 0.523 & 0.628\end{array}\right]
$](img294.svg)
![$\displaystyle {\bf H}={\bf QAQ}^T=\left[\begin{array}{rrrr}
3.000 & -1.633 & 4...
...05\\
0 & 3.184 &-3.485 & 0.211\\
0 & 0 &-1.013 & 4.652 \end{array}\right]
$](img295.svg)
 and the non-symmetric matrix
and the non-symmetric matrix  share the same eigenvalues
share the same eigenvalues
 .
.