Sensitivity and Conditioning

In numerical methods, it is important to know how reliable the numerical result produced by a certain numerical algorithm is, in terms of how sensitive it is with respect to the various perturbations caused by the inevitable noise in the given data (e.g., observational error) and computational errors in the system parameters (e.g., truncation error). The algorithm can also be considered as a generic system or function with the given data as the input and numerical result as the output. We can therefore talk about how well or ill conditioned the system is. In general, if a large difference in the output may be caused by a small change in the input/system parameters, then the result is too sensitive to the perturbations and therefore not reliable. Whether a problem is well or ill defined (the system is well or ill behaved) can therefore be measured based on such sensitivities:

• If a small change in the input causes a small change in the output, the problem is well conditioned (well behaved).
• If a small change in the input can cause a large change in the output, the problem is ill conditioned (ill behaved).

Specifically, How well or ill conditioned a problem is can be measured quantitatively by the absolute or relative condition numbers defined below:

• The absolute condition number $\hat\kappa$ is the upper bound of the ratio between the change in output and change in input:

  $$\hat\kappa\ge\frac{\vert\vert\mbox{change in output}\vert\vert}{\... ...tput}\vert\vert\; \le\; \hat\kappa\; \vert\vert\mbox{change in input}\vert\vert$$ (1)

• The relative condition number $\kappa$ is the upper bound of the ratio between the relative change in output and relative change in input:

  $$\kappa\ge\frac{\vert\vert\mbox{change in output}\vert\vert/\vert\... ...c{\vert\vert\mbox{change in input}\vert\vert}{\vert\vert\mbox{input}\vert\vert}$$ (2)

Here $\vert\vert {\bf x} \vert\vert$ is the norm of any variable ${\bf x}$ (real or complex scalar, vector, matrix, function, etc.), a real scalar representing its “size”. In the following, we will use mostly the 2-norm for any vector ${\bf x}$ and the corresponding spectral norm for any matrix ${\bf A}$. Specifically, the spectral norm $\vert\vert{\bf A}\vert\vert$ satisfies the following properties:

$$\left\{ \begin{array}{ll} \mbox{positivity:} & \vert\vert{\bf... ...bf A}\vert\vert\,\vert\vert{\bf B}\vert\vert \end{array}\right.$$ (3)

As the relative condition number compares the normalized changes in both the input and output, its value is invariant to the specific units used to measure them. The change in input can also be equivalently normalized by the input plus change $\vert\vert$input + change in input$\vert\vert$ as well as $\vert\vert$input$\vert\vert$. The same is true for the change in the output.

Obviously, the smaller the condition number, the better conditioned the problem is, the less sensitive the solution is with respect to the perturbation of the data (error, noise, approximation, etc.); and the larger the condition number, the more ill conditioned the problem is. In the following, we specifically consider the condition numbers defined for some different systems.

System with single input and output variables

A system of a single input $x$ and single output $y$ can be described by a function $y=f(x)$ to be evaluated at a given input $x$. The condition number of the function at point $x$ is defined as the greatest (worst case) ratio between the changes of the output and the input:

$$\hat\kappa=\lim_{\epsilon\rightarrow 0}\sup\limits_{\vert\delta x... ...}\frac{\vert\delta f(x)\vert/\vert f(x)\vert}{\vert\delta x\vert/\vert x\vert},$$ (4)

Here $\sup$ is the symbol for supremum (least upper bound) and $\vert x\vert$ is the norm of the scaler variable which is either the absolute value of $x$ if $x\in\mathbb{R}$ is real or modulus of $x$ if $x\in\mathbb{C}$ is complex. Note that in general the condition number is a function of $x$.

When the perturbation $\delta x$ is small, the Taylor expansion of the function can be approximated as

$$f(x+\delta x)=f(x)+f'(x)\delta x+f''(x)\frac{\delta x^2}{2}+\cdots \approx f(x)+f'(x)\delta x$$ (5)

i.e.,

$$\delta y=f(x+\delta x)-f(x)\approx f'(x)\delta x$$ (6)

Taking the absolute value or modulus on both sides, we get

$$\big\vert\delta y\big\vert=\big\vert f(x+\delta x)-f(x)\big\vert ... ...(x)\big\vert\;\big\vert\delta x\big\vert =\hat\kappa \big\vert\delta x\big\vert$$ (7)

where $\hat\kappa=\vert\delta y\vert/\vert\delta x\vert=\vert f'(x)\vert$ is the absolute condition number. Dividing both sides by $\vert y\vert=\vert f(x)\vert$, we get

$$\frac{\big\vert\delta y\big\vert}{\big\vert y\big\vert} =\frac{\v... ...rt x\big\vert} =\kappa \frac{\big\vert \delta x\big\vert}{\big\vert x\big\vert}$$ (8)

where $\kappa$ is the relative condition number:

$$\kappa\approx \frac{\vert\delta y\vert/\vert y\vert}{\vert\delta ... ...)\vert}{\vert f(x)\vert} =\frac{\vert f'(x)\vert}{\vert f(x)\vert/\vert x\vert}$$ (9)

The discussion above is for the task of evaluating the output $y=f(x)$ of a system as a function of the input $x$. However, if the task is to solve a given equation $f(x)=0$, for the purpose of finding $x$ treated as the output that satisfies the equation with $y=f(x)=0$ treated as the input, the problem needs to be converted into the form of evaluating the function $x=g(y)=f^{-1}(y)$ at $y=0$. The absolute condition number of this function $g(y)=f^{-1}(y)$ is

$$\hat\kappa=\vert g'(y)\vert=\bigg\vert\frac{d}{dy}[ f^{-1}(y)]\bigg\vert =\frac{1}{\big\vert f'(x)\big\vert}$$ (10)

which is the reciprocal of the absolute condition number $\vert f'(x)\vert$ of the corresponding evaluating problem. We therefore see that the larger $\vert f'(x)\vert$, or the smaller $g'(y)$, the better conditioned the problem is.

In the figure below, $\vert f'_1(x)\vert>\vert f'_2(x)\vert$, therefore for the problem of evaluating $y=f(x)$, $f_1(x)$ is more ill-conditioned than $f_2(x)$, but for the problem of solving $f(x)=0$, $f_1(x)$ is better conditioned than $f_2(x)$.

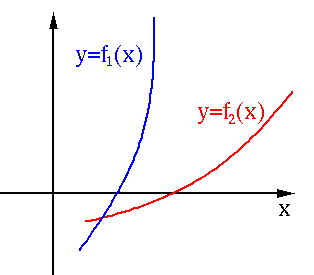
Example: Consider the following function and its derivative:

$$y=f(x)=\frac{x}{1-x},\;\;\;\;\;\;f'(x)=\frac{1}{(1-x)^2}$$ (11)

$$\begin{tabular}{c\vert\vert c\vert c\vert c\vert c} \hline x & -0... ...0.99 \\ \hline y=f(x) & -0.4975 & -0.4949 & 49.0 & 99.0 \\ \hline \end{tabular}$$ (12)

$$\kappa=\frac{\vert f'(x)\vert}{\vert f(x)\vert/\vert x\vert}=\frac{1/(1-x)^2}{\vert x/(1-x)\vert/\vert x\vert} =\frac{1}{\vert 1-x\vert}$$ (13)

• at $x=-0.99$,

  $$\kappa=\frac{1}{\vert 1-x\vert}=\frac{1}{1.99}\approx 0.5$$ (14)

  $$\vert\delta x\vert=\vert-0.99-(-0.98)\vert=0.01,\;\;\;\; \vert\delta y\vert=\vert-0.4975-(-0.4949)\vert=0.0026$$ (15)

  $$\frac{\vert\delta y\vert}{\vert\delta x\vert}=\frac{0.0026}{0.01}... ...\vert}{\vert\delta x\vert/\vert x\vert} =\frac{0.0026/0.4975}{0.01/0.99}=0.5174$$ (16)

  At this point, the problem of evaluating $y=f(x)$ is well-conditioned.

• at $x=0.99$,

  $$\kappa=\frac{\vert f'(x)\vert}{\vert f(x)\vert/\vert x\vert}=\frac{1}{\vert 1-x\vert} =\frac{1}{0.01}=100$$ (17)

  $$\vert\delta x\vert=\vert.99-0.98\vert=0.01,\;\;\;\;\vert\delta y\vert=\vert 99-49\vert=50$$ (18)

  $$\frac{\vert\delta y\vert}{\vert\delta x\vert}=\frac{50}{0.01}=500... ...vert/\vert y\vert}{\vert\delta x\vert/\vert x\vert}=\frac{50/49}{0.01/0.98}=100$$ (19)

  At this point, the function is ill-conditioned.

We see the function is well-conditioned at $x=-0.99$ but ill-conditioned at $x=0.99$.

However, the problem of solving the equation $f(x)=0$ is very ill-conditioned, as in the neighborhood of the root $x=0$, $1/f'(x)$ is very large, any value in a wide range in $x$ could result in $f(x)\approx 0$, and therefore considered as a solution, which is certainly not reliable.

Systems with Multiple input and output variables

The results above can be generalized to a system of multiple inputs ${\bf x}=[x_1,\cdots,x_N]^T$ and multiple outputs ${\bf y}=[y_1,\cdots,y_M]^T$ represented by a function ${\bf y}={\bf f}({\bf x})$. A change $\delta{\bf x}$ in the input will cause certain change in the output:

$$\delta{\bf y}={\bf f}({\bf x}+\delta{\bf x})-{\bf f}({\bf x})$$ (20)

When $\delta{\bf x}$ is small, the output can be approximated by the first two terms of its Taylor series expansion:

$${\bf f}({\bf x}+\delta{\bf x})\approx{\bf f}({\bf x})+{\bf J}_f({\bf x}) \delta{\bf x}$$ (21)

where ${\bf J}_f({\bf x})$ is the Jacobian matrix of the function, and we get

$$\vert\vert\delta{\bf y}\vert\vert=\vert\vert{\bf f}({\bf x}+\delt... ...\;\vert\vert\delta{\bf x}\vert\vert=\hat\kappa\vert\vert\delta{\bf x}\vert\vert$$ (22)

where $\hat\kappa$ is the absolute condition number defined as:

$$\hat\kappa=\vert\vert{\bf J}_f({\bf x})\vert\vert \approx\frac{\vert\vert\delta{\bf y}\vert\vert}{\vert\vert\delta{\bf x}\vert\vert}$$ (23)

Dividing both sides of the equation above by $\vert\vert{\bf y}\vert\vert=\vert\vert{\bf f}({\bf x})\vert\vert$ we get

$$\frac{\vert\vert\delta{\bf y}\vert\vert}{\vert\vert{\bf y}\vert\v... ...} =\kappa \frac{\vert\vert\delta{\bf x}\vert\vert}{\vert\vert{\bf x}\vert\vert}$$ (24)

where $\kappa$ is the relative condition number defined as:

$$\kappa =\frac{\vert\vert{\bf x}\vert\vert\;\vert\vert{\bf J}_f({\... ...bf y}\vert\vert}{\vert\vert\delta{\bf x}\vert\vert/\vert\vert{\bf x}\vert\vert}$$ (25)

In particular, consider a linear system of $N$ inputs ${\bf x}=[x_1,\cdots,x_N]^T$ and $M$ outputs ${\bf y}=[y_1,\cdots,y_M]^T$ described by

$${\bf y} = {\bf f}({\bf x})={\bf A}_{M\times N} {\bf x}$$ (26)

Consider the following two problems both associated with the linear system:

• Evaluating the matrix-vector product ${\bf y}={\bf A}{\bf x}$ as the output given ${\bf x}$ as the input, the absolute condition number is $\hat\kappa({\bf A})=\vert\vert{\bf J}_f({\bf x})\vert\vert=\vert\vert{\bf A}\vert\vert$. The relative condition number of this linear system is

  $$\kappa({\bf A})=\frac{\vert\vert{\bf x}\vert\vert\;\vert\vert{\bf... ...vert\vert\frac{\vert\vert{\bf x}\vert\vert}{\vert\vert{\bf A}{\bf x}\vert\vert}$$ (27)

  We also have

  $$\vert\vert{\bf x}\vert\vert=\vert\vert{\bf A}^{-1}{\bf A}{\bf x}\... ...le \vert\vert{\bf A}^{-1}\vert\vert\; \vert\vert{\bf A}{\bf x}\vert\vert,\;\;\; \;\;\;\; \vert\vert{\bf A}{\bf x}\vert\vert \ge \frac{\vert\vert{\bf x}\vert\vert}{\vert\vert{\bf A}^{-1}\vert\vert}$$ (28)

  Substituting this into the expression of $\kappa({\bf A})$ above we get its upper bound:

  $$\kappa({\bf A})=\vert\vert{\bf A}\vert\vert\frac{\vert\vert{\bf x... ...bf x}\vert\vert} =\vert\vert{\bf A}\vert\vert\;\vert\vert{\bf A}^{-1}\vert\vert$$ (29)

  Note that $\kappa$ is no less than 1:

  $$\kappa({\bf A})=\vert\vert{\bf A}^{-1}\vert\vert\;\vert\vert{\bf ... ...vert \ge \vert\vert{\bf A}^{-1}{\bf A}\vert\vert =\vert\vert{\bf I}\vert\vert=1$$ (30)

• Solving the linear equation system ${\bf A}{\bf y}={\bf x}$ for ${\bf y}$ as the output given ${\bf x}$ as the input (for uniqueness of the solution we assume $M=N$, i.e., ${\bf A}$ is an invertible square matrix), we need to consider the inverse function ${\bf x}={\bf g}({\bf x})={\bf A}^{-1}{\bf x}$. The absolute condition number is $\hat\kappa({\bf A})=\vert\vert{\bf J}_g({\bf x})\vert\vert=\vert\vert{\bf A}^{-1}\vert\vert$. To find the relative condition number $\kappa({\bf A})$, we note that some change $\delta{\bf y}$ in the output ${\bf y}$ may be caused by perturbation $\delta{\bf A}$ in the coefficient matrix ${\bf A}$ as well as $\delta{\bf x}$ in the input ${\bf x}$, i.e.,

  $$({\bf A}+\delta{\bf A})({\bf y}+\delta{\bf y}) ={\bf x}+\delta{\bf x}$$ (31)

  Expanding the left-hand side we get

  $${\bf A}{\bf y}+{\bf A}\delta{\bf y}+\delta{\bf A}{\bf y}+\delta{\bf A}\delta{\bf y} ={\bf x}+\delta{\bf x}$$ (32)

  Subtracting ${\bf A}{\bf y}={\bf x}$ from the two sides we get

  $${\bf A}\delta{\bf y}+\delta{\bf A}{\bf y}+\delta{\bf A}\delta{\bf y} =\delta{\bf x}$$ (33)

  i.e.,

  $$\delta{\bf y}={\bf A}^{-1}(\delta{\bf x}-\delta{\bf A}{\bf y}-\delta{\bf A}\delta{\bf y})$$ (34)

  Taking norm on both sides, we get
  

  $$\vert\vert\delta{\bf y}\vert\vert \le \vert\vert{\bf A}^{-1}\vert\vert\;\vert\vert\delta{\bf x}-(\delta{\bf A}{\bf y}+\delta{\bf A}\delta{\bf y})\vert\vert$$

  $$\le \vert\vert{\bf A}^{-1}\vert\vert\;\left(\vert\vert\delta{\bf x}\v... ...rt+\vert\vert(\delta{\bf A}{\bf y}+\delta{\bf A}\delta{\bf y})\vert\vert\right)$$

  $$\le \vert\vert{\bf A}^{-1}\vert\vert\;\left(\vert\vert\delta{\bf x}\v... ...rt +\vert\vert\delta{\bf A}\vert\vert\;\vert\vert\delta{\bf y}\vert\vert\right)$$ (35)

  
  where we have used $\vert\vert{\bf x}-{\bf y}\vert\vert\le\vert\vert{\bf x}\vert\vert+\vert\vert{\bf y}\vert\vert$, $\vert\vert{\bf x}+{\bf y}\vert\vert\le\vert\vert{\bf x}\vert\vert+\vert\vert{\bf y}\vert\vert$, and $\vert\vert{\bf A}{\bf x}\vert\vert\le\vert\vert{\bf A}\vert\vert\;\vert\vert{\bf x}\vert\vert$.

  Subtracting $\vert\vert{\bf A}^{-1}\vert\vert\;\vert\vert\delta{\bf A}\vert\vert\;\vert\vert\delta{\bf y}\vert\vert$ from both sides

  $$(1-\vert\vert{\bf A}^{-1}\vert\vert\;\vert\vert\delta{\bf A}\vert... ...bf x}\vert\vert+\vert\vert\delta{\bf A}\vert\vert\;\vert\vert{\bf y}\vert\vert)$$ (36)

  and dividing both sides by $(1-\vert\vert{\bf A}^{-1}\vert\vert\;\vert\vert\delta{\bf A}\vert\vert)\;\vert\vert{\bf y}\vert\vert$, assuming $\vert\vert{\bf A}^{-1}\vert\vert\;\vert\vert\delta{\bf A}\vert\vert<1$, we get
  

  $$\frac{\vert\vert\delta{\bf y}\vert\vert}{\vert\vert{\bf y}\vert\vert} \le \frac{\vert\vert{\bf A}^{-1}\vert\vert}{1-\vert\vert{\bf A}^{-1}\... ...t}+\frac{\vert\vert\delta{\bf A}\vert\vert}{\vert\vert{\bf A}\vert\vert}\right)$$

  $$\le \frac{\vert\vert{\bf A}^{-1}\vert\vert\;\vert\vert{\bf A}\vert\ve... ...t}+\frac{\vert\vert\delta{\bf A}\vert\vert}{\vert\vert{\bf A}\vert\vert}\right)$$ (37)

  
  where we have used $\vert\vert{\bf x}\vert\vert=\vert\vert{\bf A}{\bf y}\vert\vert\le\vert\vert{\bf A}\vert\vert\;\vert\vert{\bf y}\vert\vert$, and $\kappa({\bf A})=\vert\vert{\bf A}^{-1}\vert\vert\;\vert\vert{\bf A}\vert\vert$.

  In particular,

  • if $\delta{\bf A}=0$,

    $$\frac{\vert\vert\delta{\bf y}\vert\vert}{\vert\vert{\bf y}\vert\v... ...a({\bf A})\frac{\vert\vert\delta{\bf x}\vert\vert}{\vert\vert{\bf x}\vert\vert}$$ (38)

  • if $\delta{\bf x}=0$,

    $$\frac{\vert\vert\delta{\bf y}\vert\vert}{\vert\vert{\bf y}\vert\v... ...ert\vert} \frac{\vert\vert\delta{\bf A}\vert\vert}{\vert\vert{\bf A}\vert\vert}$$ (39)

We see that both the evaluation and equation solving problems ( $\delta{\bf A}=0$) have the same relative condition number $\kappa({\bf A})=\vert\vert{\bf A}\vert\vert\;\vert\vert{\bf A}^{-1}\vert\vert$. Let the singular values of ${\bf A}$ be $\{\sigma_{max}=\sigma_1\ge\cdots\ge\sigma_n=\sigma_{min}\}$, then the singular values of ${\bf A}^{-1}$ are $\{1/\sigma_n\ge\cdots\ge 1/\sigma_1\}$, and their spectral norms are their respective greatest singular values: $\vert\vert{\bf A}\vert\vert=\sigma_{max}=\sigma_1$ and $\vert\vert{\bf A}^{-1}\vert\vert=1/\sigma_{min}=1/\sigma_n$. Now we have

$$\kappa({\bf A})=\vert\vert{\bf A}\vert\vert\;\vert\vert{\bf A}^{-1}\vert\vert=\frac{\sigma_{max}}{\sigma_{min}}$$ (40)

We see that the condition number of ${\bf A}$ is large if its $\sigma_{max}$ and $\sigma_{min}$ are far apart in values, but it is small otherwise.

The condition number $\kappa({\bf A})$ is a measurement of how close ${\bf A}$ is to singularity. When ${\bf A}$ is singular, one or more of its singular values are zero, i.e., $\sigma_{min}=0$, then $\kappa({\bf A})=\infty$, i.e., any problem ${\bf Ax}={\bf y}$ associated with a singular matrix is worst conditioned. On the other hand, as all singular values of an identity matrix ${\bf I}$ are 1, its condition number is $\kappa({\bf I})=1$, the smallest condition number possible, i.e., any problem ${\bf Ix}={\bf y}$ is best conditioned.

In Matlab, the function cond(A,p) generates the condition number of matrix A based on its p-norm. When $p=2$, this is the ratio between the greatest and smallest singular values. The following Matlab commands give the same result:

• cond(A,2)
• norm(A,2)*norm(inv(A),2)
• s=svd(A), s(1)/s(end)

We now further consider the worst case scenarios for both evaluating the matrix-vector product ${\bf y}={\bf A}{\bf x}$ and solving the linear equation system ${\bf x}={\bf A}{\bf y}$. In both cases, we find ${\bf y}$ as the output given ${\bf x}$ as the input. To do so, we first carry out the SVD decomposition of ${\bf A}$ to get ${\bf A}={\bf U}{\bf\Sigma}{\bf V}^*$ with the singular values in ${\bf\Sigma}$ sorted in descending order: $\sigma_1\ge\cdots\ge\sigma_n$. The inverse of ${\bf A}$ can also be SVD decomposed: ${\bf A}^{-1}={\bf V}{\bf\Sigma}^{-1}{\bf U}^*$.

• The worst case for evaluating ${\bf y}={\bf A}{\bf x}$:

  If ${\bf x}={\bf v}_n$ is the minimum right singular vector corresponding to the smallest singular value $\sigma_n=\sigma_{min}$. The equation becomes:
  

  $${\bf y} = {\bf A}{\bf x}=({\bf U}{\bf\Sigma}{\bf V}^*)\;{\bf v}_n ={\bf U}{... ..._n\end{array}\right] \left[\begin{array}{c}0\\ \vdots\\ 0\\ 1\end{array}\right]$$

  $$= [{\bf u}_1,\cdots,{\bf u}_n] \left[\begin{array}{c}0\\ \vdots\\ 0\\ \sigma_n\end{array}\right] =\sigma_n{\bf u}_n$$ (41)

  
  and

  $${\bf y}+\delta{\bf y}={\bf A}({\bf x}+\delta{\bf x}) =\sigma_n{\bf u}_n+{\bf A}\delta{\bf x}$$ (42)

  The absolute error $\vert\vert\delta{\bf y}\vert\vert=\vert\vert{\bf A}\delta{\bf x}\vert\vert$ may be small if $\delta{\bf x}$ is small, but the relative error $\vert\vert\delta{\bf y}\vert\vert/\vert\vert{\bf y}\vert\vert$ may be large as $\vert\vert{\bf y}\vert\vert=\vert\sigma_n\vert\,\vert\vert{\bf u}\vert\vert$ is small when $\sigma_n=\sigma_{min}$ is small (e.g., close to zero).

• The worst case for solving ${\bf x}={\bf A}{\bf y}$:

  If ${\bf x}={\bf u}_1$ is the maximum left singular vector corresponding to the largest singular value $\sigma_1=\sigma_{max}$. The equation becomes:
  

  $${\bf y} = {\bf A}^{-1}{\bf x}={\bf V}{\bf\Sigma}^{-1}{\bf U}^*{\bf u}_1 ={\... ..._n\end{array}\right] \left[\begin{array}{c}1\\ 0\\ \vdots\\ 0\end{array}\right]$$

  $$= [{\bf v}_1,\cdots,{\bf v}_n] \left[\begin{array}{c}1/\sigma_1\\ 0\\ \vdots\\ 0\end{array}\right] =\frac{1}{\sigma_1}{\bf v}_1$$ (43)

  
  and

  $${\bf y}+\delta{\bf y}={\bf A}^{-1}({\bf x}+\delta{\bf x}) =\frac{1}{\sigma_1}{\bf v}_1+{\bf A}^{-1}\delta{\bf x}$$ (44)

  The absolute error $\vert\vert\delta{\bf y}\vert\vert=\vert\vert{\bf A}^{-1}\delta{\bf x}\vert\vert$ may be small if $\delta{\bf x}$ is small, but the relative error $\vert\vert\delta{\bf y}\vert\vert/\vert\vert{\bf y}\vert\vert$ may be large as $\vert\vert{\bf y}\vert\vert=\vert\vert{\bf u}\vert\vert/\vert\sigma_1\vert$ is small when $\sigma_1=\sigma_{max}$ is large.

Example 1: Consider solving the linear system ${\bf A}{\bf x}={\bf b}$ with

$${\bf A}=\frac{1}{2}\left[\begin{array}{rr}3.0 & 2.0\\ 1.0 & 4.0\e... ...; {\bf A}^{-1}=\left[\begin{array}{rr}0.8 & -0.4\\ -0.2 & 0.6\end{array}\right]$$ (45)

The singular values of ${\bf A}$ are $\sigma_1=2.5583$ and $\sigma_2=0.9772$, the condition number is

$$\kappa=\vert\vert{\bf A}\vert\vert\;\vert\vert{\bf A}^{-1}\vert\vert=\frac{\sigma_1}{\sigma_2}=2.618$$ (46)

which is small, indicating this is a well-behaved system. Given two similar inputs ${\bf b}_1=[1,\;1]^T$ and ${\bf b}_2=[0.99,\;1.01]^T$ with $\delta{\bf b}=[0.01,\;-0.01]^T$, we find the corresponding solutions:

$${\bf x}_1={\bf A}^{-1}{\bf b}_1 =\left[\begin{array}{r}0.4 // 0.4... ...;\;\;\;\; \delta{\bf x}=\left[\begin{array}{r}0.012 \\ -0.008\end{array}\right]$$ (47)

We have

$$\vert\vert\delta{\bf b}\vert\vert=0.0141,\;\;\;\;\vert\vert{\bf b... ...vert\delta{\bf x}\vert\vert=0.0144,\;\;\;\;\vert\vert{\bf x}_1\vert\vert=0.5657$$ (48)

and

$$\frac{\vert\vert\delta{\bf x}\vert\vert/\vert\vert{\bf x}_1\vert\... ...lta{\bf b}\vert\vert/\vert\vert{\bf b}_1\vert\vert} =\frac{0.0255}{0.01}=2.5495$$ (49)

Example 2:

$${\bf A}=\frac{1}{2}\left[\begin{array}{rr}1.000 & 1.000\\ 1.001 &... ...\bf A}^{-1}=\left[\begin{array}{rr}-999 & 1000\\ 1001 & -1000\end{array}\right]$$ (50)

The singular values of ${\bf A}$ are $\sigma_1=1.0$ and $\sigma_2=0.0005$, the condition number is

$$\kappa=\vert\vert{\bf A}\vert\vert\;\vert\vert{\bf A}^{-1}\vert\vert=\frac{\sigma_1}{\sigma_2}=2000$$ (51)

indicating matrix ${\bf A}$ is close to singularity, and the system is ill-conditioned. The solutions corresponding to the same two inputs ${\bf b}_1=[1,\;1]^T$ and ${\bf b}_2=[0.99,\;1.01]^T$ are

$${\bf x}_1={\bf A}^{-1}{\bf b}_1 =\left[\begin{array}{r}1 \\ 1\end... ...;\;\;\;\; \delta{\bf x}=\left[\begin{array}{r}-19.99 \\ 20.01\end{array}\right]$$ (52)

We can further find

$$\vert\vert\delta{\bf b}\vert\vert=0.0141,\;\;\;\;\vert\vert{\bf b... ...ert\delta{\bf x}\vert\vert=28.2843,\;\;\;\;\vert\vert{\bf x}_1\vert\vert=1.4142$$ (53)

and the condition number is:

$$\frac{\vert\vert\delta{\bf x}\vert\vert/\vert\vert{\bf x}_1\vert\... ...rt\delta{\bf b}\vert\vert/\vert\vert{\bf b}_1\vert\vert} =\frac{200}{0.01}=2000$$ (54)

We see that a small relative change $\vert\vert\delta{\bf b}\vert\vert/\vert\vert{\bf b}_1\vert\vert=0.01$ in the input caused a huge change $\vert\vert\delta{\bf x}\vert\vert/\vert\vert{\bf x}_1\vert\vert=20$ in the output (2000 times greater).

Example 3: Consider

$${\bf A}=\left[ \begin{array}{ll} 3.1 & 2.0\\ 6.0 & 3.9\end{array}... ...ight] \left[\begin{array}{rr}-0.839 & -0.544\\ -0.544 & 0.839\end{array}\right]$$ (55)

with

$$\vert\vert{\bf A}\vert\vert=\sigma_1=8.05,\;\;\;\;\;\vert\vert{\b... ...;\; \kappa=\vert\vert{\bf A}\vert\vert\;\vert\vert{\bf A}^{-1}\vert\vert=720.22$$ (56)

As ${\bf A}$ is near singular, its condition number $\kappa$ is large, indicating that the problem associated with this ${\bf A}$ is ill-conditioned. We will now specifically consider both problems of evaluating and solving the linear system.

• Solve ${\bf Ay}={\bf x}$ for ${\bf y}$ given ${\bf x}$:

  $${\bf y}+\delta{\bf y}={\bf A}^{-1}({\bf x}+\delta{\bf x}),\;\;\;\;\; \delta{\bf y}={\bf A}^{-1} \delta{\bf x}$$ (57)

  The absolute condition number is $\hat\kappa=\vert\vert{\bf A}^{-1}\vert\vert=89.46$. The change in output ${\bf y}$ is

  $$\vert\vert\delta{\bf y}\vert\vert\le \vert\vert{\bf A}^{-1}\vert\... ...ppa\;\vert\vert\delta{\bf x}\vert\vert=89.46\;\vert\vert\delta{\bf x}\vert\vert$$ (58)

  which is $\hat\kappa=89.46$ times greater than any change $\delta{\bf x}$ in the input. We further consider the worst case when ${\bf x}={\bf u}_{max}$ and the relative error:

  $${\bf x}={\bf u}_1=\left[\begin{array}{rr}-0.458\\ -0.889\end{arra... ...}={\bf A}^{-1}{\bf x} =\left[\begin{array}{rr}-0.104\\ -0.068\end{array}\right]$$ (59)

  Even for a small change $\delta{\bf x}$ in the input, causing a small change $\delta{\bf y}$ in the output:

  $$\delta{\bf x}=\left[\begin{array}{rr}0.01\\ -0.01\end{array}\righ... ...f A}^{-1}\delta{\bf x} =\left[\begin{array}{rr}0.656\\ -1.011\end{array}\right]$$ (60)

  the ratios of the absolute and relative errors are:

  $$\frac{\vert\vert\delta{\bf y}\vert\vert}{\vert\vert\delta{\bf x}\... ...a{\bf x}\vert\vert/\vert\vert{\bf x}\vert\vert} =\frac{9.702}{0.014}\approx 686$$ (61)

• Evaluate ${\bf y}={\bf A}{\bf x}$ given ${\bf x}$:

  $${\bf y}+\delta{\bf y}={\bf A}({\bf x}+\delta{\bf x}),\;\;\;\;\; \delta{\bf y}={\bf A} \delta{\bf x}$$ (62)

  The absolute condition number is $\hat\kappa=\vert\vert{\bf A}\vert\vert=8.05$. The absolute change in output ${\bf y}$ is

  $$\vert\vert\delta{\bf y}\vert\vert\le\vert\vert{\bf A}\vert\vert\;\vert\vert\delta{\bf x}\vert\vert=8.051\;\vert\vert\delta{\bf x}\vert\vert$$ (63)

  which is not too much greater than the absolute change $\delta{\bf x}$ in the input. However, a much greater relative error will result if we consider the worst case when ${\bf x}={\bf v}_{min}$:

  $${\bf x}={\bf v}_2=\left[\begin{array}{rr}-0.5444\\ 0.8388\end{arr... ...bf y}={\bf A}{\bf x} =\left[\begin{array}{rr}-0.0099\\ 0.0051\end{array}\right]$$ (64)

  Even for a small change $\delta{\bf x}$ in the input, causing a small change $\delta{\bf y}$ in the output:

  $$\delta{\bf x}=\left[\begin{array}{rr}0.01\\ -0.01\end{array}\righ... ...y}={\bf A}\delta{\bf x} =\left[\begin{array}{rr}0.011\\ 0.021\end{array}\right]$$ (65)

  The ratios of the absolute and relative errors are:

  $$\frac{\vert\vert\delta{\bf y}\vert\vert}{\vert\vert\delta{\bf x}\... ...bf x}\vert\vert/\vert\vert{\bf x}\vert\vert} =\frac{2.1207}{0.0141} \approx 150$$ (66)

  Although the ratio of the absolute errors is small, the ratio of the relative errors is large.

Associated with whether a problem is well or ill conditioned is the issue of an approximate solutions. For the problem of solving an equation system ${\bf f}({\bf x})={\bf0}$, there exist two types of approximate solutions:

• The approximate solution corresponds to a small residual in the image of the function:

  $$\vert\vert{\bf f}(\hat{\bf x})\vert\vert\approx 0$$ (67)

• The approximate solution $\hat{\bf x}$ is close to the true solution ${\bf x}^*$ satisfying ${\bf f}({\bf x}^*)={\bf0}$ (typically unknown) in the domain of the function:

  $$\vert\vert\hat{\bf x}'-{\bf x}^*\vert\vert\approx 0$$ (68)

If the problem is well-conditioned, the two different criteria are consistent, i.e., the two approximations are similar, $\vert\vert\hat{\bf x}-\hat{\bf x}'\vert\vert$ is small. However, if the problem is ill-conditioned, they can be very different.