


Next: About this document ...
Up: svd
Previous: Conservation of Degrees of
SVD image transform has different applications in image processing and
analysis. We now consider how it can be used for data compression.
First we write a matrix 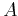 as
as
where
![${\bf a}_i=[a(1,i),\cdots,a(N,i)]^T$](img48.png) is the ith column vector of
is the ith column vector of 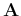 .
The total amount of energy contained in
.
The total amount of energy contained in 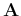 can be represented by the
norm of
can be represented by the
norm of 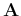 defined as
defined as
Now we consider image compression achieved by using only the first
eigenimages of the given image 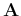 :
:
with error
After compression, the energy (information) contained in is:
Note that here we have used the property that
.
We see that the total amount of energy (information) contained in the
original image 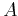 is
is
and the energy (information) lost (contained in ) is
It is therefore obvious that minimum energy is lost if we range
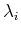 's so that
's so that
To find out the compression ratio, consider total degrees of freedom in
:
The degrees of freedom in the orthogonal vectors
are
The same is true for
. Including the
degrees of freedom in
, we have the total d.o.f.:
and the compression ratio is
An example of using SVD for image compression is available
here



Next: About this document ...
Up: svd
Previous: Conservation of Degrees of
Ruye Wang
2015-05-15
![]() as
as