


Next: Conservation of Degrees of
Up: svd
Previous: svd
Let the 2D image array be represented by a matrix
![${\bf A}=[ a_{ij} ]_{M\times N}$](img1.png) with rank equal to
with rank equal to 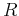 . Here we assume
. Here we assume
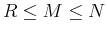 . Now we consider the
following eigenvalue problems for the matrix
. Now we consider the
following eigenvalue problems for the matrix 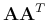 and
matrix
and
matrix
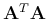 :
:
where and are M-D and N-D eigenvectors of
and
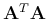 , respectively, and
, respectively, and
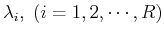 are the eigenvalues of both
are the eigenvalues of both 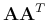 and
and
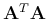 .
.
Since these matrices are symmetric, their eigenvectors are orthogonal:
and they form two orthogonal matrices
![$ {\bf U}=[{\bf u}_1,\cdots,{\bf u}_N]_{M\times M}$](img14.png) and
and
![$ {\bf V}=[{\bf v}_1,\cdots,{\bf v}_N]_{N\times N} $](img15.png) and
and
As there exist only 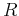 non-zero eigenvalues,
non-zero eigenvalues,
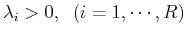 , both matrices
, both matrices 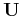 and
and 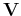 have
some zero columns and the matrix
have
some zero columns and the matrix 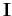 has only
has only 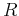 non-zero diagonal elements.
non-zero diagonal elements.
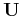 and
and 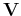 will diagonalize
will diagonalize 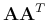 and
and
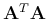 respectively:
respectively:
and
From linear algebra, we know that the singular value decomposition (SVD)
of 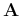 is defined as:
is defined as:
This can be considered as the forward SVD transform and the inverse transform
can be obtained by left multiplying
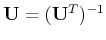 and right multiplying
and right multiplying
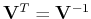 both sides of the equation above:
both sides of the equation above:
This inverse SVD transform can be so interpreted that the original image
matrix is decomposed into a set of  eigenimages
eigenimages
![$\sqrt{\lambda_i}[{\bf u}_i{\bf v}_i^T]$](img28.png) , where the outer product
, where the outer product
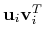 is an M by N matrix.
is an M by N matrix.
SVD transform pair:
Example: The Lenna image 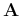 together with its
together with its 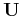 ,
, 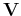 matrices and singular values (
matrices and singular values (
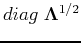 ):
):




The first 10 eigen-images of the Lenna image:

More of the eigen-images (from 10 to 120 with increment of 10):

First 10 partial sum images:

The partial sum images (from 10 to 120 eigen-images with increment 10):




Next: Conservation of Degrees of
Up: svd
Previous: svd
Ruye Wang
2015-05-15
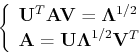
![]() together with its
together with its ![]() ,
, ![]() matrices and singular values (
matrices and singular values (
![]() ):
):







